
【题目】在“学本课堂”的实践中,王老师经常让学生以“问题”为中心进行自主、合作、探究学习.
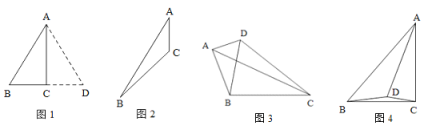
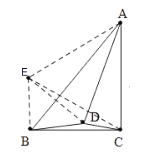
(课堂提问)王老师在课堂中提出这样的问题:如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,那么BC和AB有怎样的数量关系?
(互动生成)经小组合作交流后,各小组派代表发言.
(1)小华代表第3小组发言:AB=2BC. 请你补全小华的证明过程.
证明:把△ABC沿着AC翻折,得到△ADC.
∴∠ACD=∠ACB=90°,
∴∠BCD=∠ACD+∠ACB=90°+90°=180°,
即:点B、C、D共线.(请在下面补全小华的证明过程)
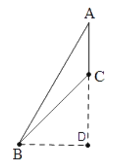
(2)受到第3小组“翻折”的启发,小明代表第2小组发言:如图2,在△ABC中,如果把条件“∠ACB=90°”改为“∠ACB=135°”,保持“∠BAC=30°”不变,若BC=1,求AB的长.
(思维拓展)如图3,在四边形ABCD中,∠BCD=45°,∠BAD=90°,∠ADB=∠CDB=60°,且AC=3,则△ABD的周长为 .
(能力提升)如图4,点D是△ABC内一点,AD=AC,∠BAD=∠CAD=20°,∠ADB+∠ACB=210°,则AD、DB、BC三者之间的相等关系是 .
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ;(4)DB2+BC2=AD2.
;(4)DB2+BC2=AD2.
【解析】
(1)根据提示证明出△ABD为等边三角形即可说明BC和AE的关系;
(2)过点B作AC边的垂线,交AC的延长线于点D ,设![]() ,则
,则![]() ,解出
,解出![]() 即可;
即可;
(3)思维拓展:作BD⊥CD于点E ,作CF垂直AD的延长线于点F,设![]() ,
,![]() ,然后表示出
,然后表示出![]() ,
,![]() 边建立方程解出
边建立方程解出![]() 即可.
即可.
(4)能力提升:把△ABD沿AB边翻折得到△AEB,连接ED , EC ,先通过角度转换得到![]() 再证明
再证明![]() ,
,![]() ,即可求出AD、DB、BC三 边的关系;
,即可求出AD、DB、BC三 边的关系;
(1)证明:把△ABC沿AC翻折,得到△ADC,
∴∠ACD=∠ACB=90°,
∴∠BCD=∠ACD+∠ACB=90°+90°=180°,
即:点B、C、D共线,
∴AB=AD,
∵∠BAC=30°,
∴∠ABC=60°,
∴△ABD为等边三角形,
∴AB=BD=2BC.
(2)过点B作AC边的垂线,交AC的延长线于点D,
∵∠ACB=135°,
∴∠BCD=45°,
∵∠BDC=90°,BC=1,
设BD=![]() ,则CD=BC=
,则CD=BC=![]() ,
,
![]() ,
,
解得:![]() ,
,
∵∠BAC=30°,
∴ AB=2BD=![]() .
.
思维拓展:
(3)作BD⊥CD于点E ,作CF垂直AD的延长线于点F ,
∵∠BAD=90°,∠ADB=∠CDB=60°,
∴△BAD≌△BED,
∵∠BCD=45° ,
∴BE=CE,
设AD=x ,
∴BD= 2AD=2x ,
∴![]() ,
,
∴EC=EB=AB=![]()
![]() ,
,
∴![]()
∴∠FDC=60°,∠ECD=30°,
∴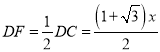 ,
,
∴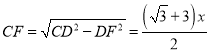 ,
,
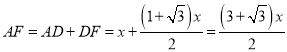
∵AC=1,
在![]() 中,
中, ![]() ,
,
则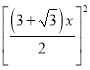
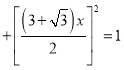 ,
,
解得:![]() ,
,
![]() ,
,
![]() ,
,
则△ABD的周长为:![]() .
.
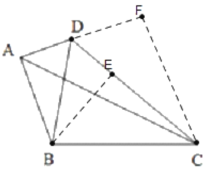
(4)能力提升:
把△ABD沿AB边翻折得到△AEB,连接ED,EC,
∵∠BAD=∠CAD=20°,
∴∠EAB=20°,
∴∠EAC=60°,
∵∠ACB+∠ADB=210°, ∠AEB=∠ADB,
∴∠ACB=∠AEB=210°,
∴∠EBC=360°-210°-60°=90°,
∵AD=AC,AE=AD,
∴AE=AC,
∴△AEC为等腰三角形,
∴EC=AE=AD,
在![]() 中,
中,![]() ,
,
∵EB=BD,EC=AD,
∴![]() .
.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形![]() 的边长
的边长![]() .某一时刻,动点
.某一时刻,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动;同时,动点
点匀速运动;同时,动点![]() 从
从![]() 点出发沿
点出发沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 点匀速运动,问:
点匀速运动,问:
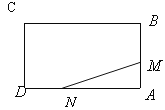
(1)经过多少时间,![]() 的面积等于矩形
的面积等于矩形![]() 面积的
面积的![]() ?
?
(2)是否存在时间t,使![]() 的面积达到3.5cm2,若存在,求出时间t,若不存在,说明理由.
的面积达到3.5cm2,若存在,求出时间t,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2﹣3x+4.
x2﹣3x+4.
(1)配方成y=a(x﹣h)2+k的形式;
(2)求出它的图象的开口方向对称轴顶点坐标;
(3)求当y<0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+1与双曲线相交于点A(m,![]() )与x轴交于点 B.
)与x轴交于点 B.
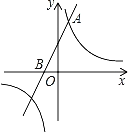
(1)求双曲线的函数表达式:
(2)点P在x轴上,如果△ABP的面积为6,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年九龙口诗词大会在九龙口镇召开,我校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.
(1)若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;
(2)若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是ts(0<t≤15),过点D作DF⊥BC于点F,连接DE,EF,若四边形AEFD为菱形,则t的值为( )
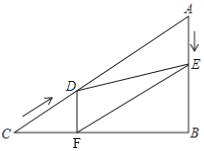
A.20B.15C.10D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.
(1)若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?
(2)在(1)的条件下,当该这种书包销售单价为多少元时,销售利润是3120元?
(3)这种书包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市连续5天的天气情况.

(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据如图提供的信息,请再写出两个不同类型的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com