
【题目】某高科技公司根据市场需求,计划生产A,B两种型号的医疗器械.其部分信息如下:
信息一:每台A型器械的售价为24万元,每台B型器械的售价为30万元,每台B型器械的生产成本比A型器械的生产成本多5万元.
信息二:若销售3台A型器械和5台B型器械,共获利37万元;
根据上述信息,解答下列问题:
(1)求每台A型器械、每台B型器械的生产成本各是多少万元?
(2)若A,B两种型号的医疗器械共生产80台,且该公司所筹生产医疗器械资金不少于1800万元,但不超过1810万元,且把所筹资金全部用于生产此两种医疗器械,根据市场调查,每台A型医疗器械的售价将会提高a万元(a>0),每台B型医疗器械的售价不会改变,该公司应该如何生产可以获得最大利润?
【答案】(1)每台A型器械的生产成本是20万元,则每台B型器械的生产成本是25万元;(2)当a>1时,生产A种器械40台,B种器械40台,获得最大利润,当a=1时,三种方案利润都为400万元;当0<a<1时,生产A种器械38台,B种器械42台,获得最大利润.
【解析】
(1)设每台A型器械的生产成本是y万元,则每台B型器械的生产成本是(y+5)万元,(2)根据“销售3台A型器械和5台B型器械,共获利37万元”。列出方程,即可求解;
(3)设该公司生产A种疗器械x台,则生产B种医疗器械(80-x)台,列出不等式组,求出x的范围,再取整数,根据条件,得到利润关于x的函数,对参数a分类讨论,即可得到结论.
(1)设每台A型器械的生产成本是y万元,则每台B型器械的生产成本是(y+5)万元,
依题意得:3(24-y)+5[30-(y+5)]=37,
解得:y=20,
y+5=20+5=25,
答:每台A型器械的生产成本是20万元,则每台B型器械的生产成本是25万元;
(2)设该公司生产A种疗器械x台,则生产B种医疗器械(80-x)台,
依题意得: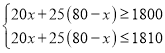 ,
,
解得38≤x≤40,
取整数得:x=38,39,40,
∴该公司有3种生产方案:
方案一:生产A种器械38台,B种器械42台.
方案二:生产A种器械39台,B种器械41台.
方案三:生产A种器械40台,B种器械40台.
依题意得,W=(24-20+a)x+(30-25)(80-x)=(4+a)x+400-5x=(a-1)x+400,
当a-1>0,即a>1时,生产A种器械40台,B种器械40台,获得最大利润,
当a-1=0,即a=1时,三种方案利润都为400万元;
当a-1<0,即0<a<1时,生产A种器械38台,B种器械42台,获得最大利润.


科目:初中数学 来源: 题型:
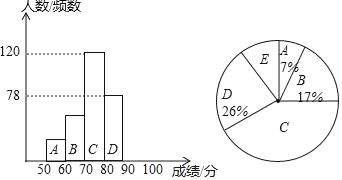
【题目】近日,深圳市人民政府发布了《深圳市可持续发展规划》,提出了要做可持续发展的全球创新城市的目标,某初中学校了解学生的创新意识,组织了全校学生参加创新能力大赛,从中抽取了部分学生成绩,分为5组:A组50~60;B组60~70;C组70~80;D组80~90;E组90~100,统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.
(1)抽取学生的总人数是 人,扇形C的圆心角是 °;
(2)补全频数直方图;
(3)该校共有2200名学生,若成绩在70分以下(不含70分)的学生创新意识不强,有待进一步培养,则该校创新意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为合理开展“体艺2+1”活动,随机抽取部分学生进行问卷调查(每位学生只选择一种自己喜欢的项目),并将调查的结果绘制成如下的两幅不完整的统计图.
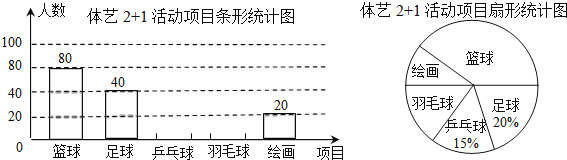
请根据图中提供的信息,解答下面的问题:
(1)参加调查的学生有 人,在扇形统计图中,表示 参加“绘画”学生的扇形的圆心角为 ;
(2)将条形统计图补充完整;
(3)若该中学有1 450名学生,则估计该中学喜欢“篮球”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
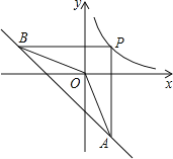
【题目】如图,P为反比例函数y=![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-6的图象于点A、B.若∠AOB=135°,则k的值是______.
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-6的图象于点A、B.若∠AOB=135°,则k的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的业余文化生活,某校教务处准备在大课间期间开设兴趣小组,预设科目为“舞蹈”“音乐”“电竞”“动漫”为了准确配备教室与师资,负责人制作了“你最喜欢的科目”的调查问卷,在校园随机调查后制作了两幅不完整的统计图,请你根据信息解答下面问题:
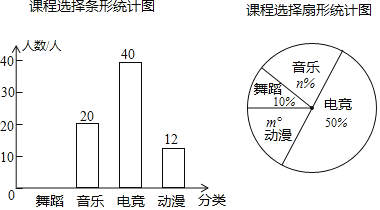
(1)本次调查中,参与问卷调查的人数为 ;
(2)扇形统计图中的m、n的值为 、 ,补全条形统计图;
(3)若该校有学生2000人,请你估计报名“电竞”的学生的人数为 ;
(4)最先报名“动漫”课程的三名学生中有两名男生一名女生,若随机抽取两名学生参与教室网线布设,求两名学生恰为一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=9,S△ABC=![]() ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
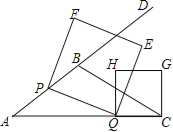
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com