
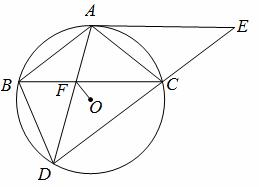
如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
(1)求证:四边形ABCE是平行四边形;
(2)若AE=6,CD=5,求OF的长.
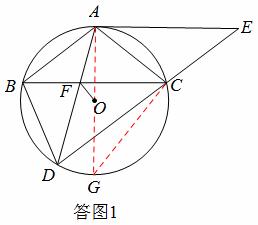
解:(1)证明:如答图1,连接AO并延长交⊙O于另一点G,连接CG,
∵AE是⊙O的切线,∴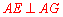 .
.
∴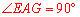 ,即
,即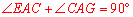 .
.
∵AO是⊙O的直径,∴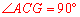 .
.
∴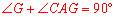 .
.
∴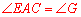 .
.
∵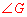 和
和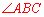 是同圆中同弧所对的圆周角,
是同圆中同弧所对的圆周角,
∴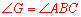 .
.
∴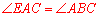 .
.
(学习过弦切角定理的直接得此)
∵AB=AC,∴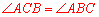 .∴
.∴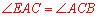 .∴AE∥BC.
.∴AE∥BC.
又∵AB∥CD,∴四边形ABCE是平行四边形.
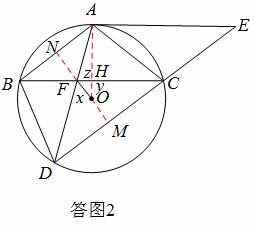
(2)如答图2,连接AO,交BC于点H,双向延长OF分别交AB、CD于点N、M,
∵AE是⊙O的切线,
∴根据切割线定理,得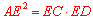 ,(没学习切割线定理可由相似得到)
,(没学习切割线定理可由相似得到)
∵ AE=6,CD=5,∴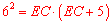 ,解得
,解得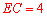 (已舍去负数).
(已舍去负数).
由圆的对称性,知四边形ABDC是等腰梯形,且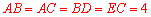 .
.
又根据对称性和垂径定理,知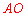 垂直平分
垂直平分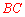 ,
,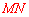 垂直平分
垂直平分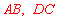 .
.
设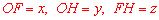 ,
,
∵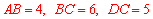
∴ .
.
易证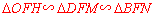 ,
,
∴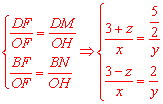 .
.
两式相加和相除,得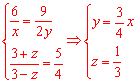 .
.
又∵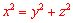 ,∴
,∴ .
.
∴OF的长为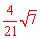 .
.
‘
【考点】切线的性质;圆周勾股定理;等腰三角形的性质;平行的判定;平行四边形的判定和性质;等腰梯形的判定和性质;垂径定理;相似判定和性质;勾股定理.
【分析】(1)作辅助线,连接AO并延长交⊙O于另一点G,连接CG,根据切线的性质证明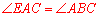 ,根据等腰三角形等边对等角的性质和等量代换得到
,根据等腰三角形等边对等角的性质和等量代换得到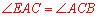 ,从而根据内错角相等两直线平行的判定得到AE∥BC,结合已知AB∥CD即可判定四边形ABCE是平行四边形.
,从而根据内错角相等两直线平行的判定得到AE∥BC,结合已知AB∥CD即可判定四边形ABCE是平行四边形.
(2)作辅助线,连接AO,交BC于点H,双向延长OF分别交AB、CD于点N、M,根据切割线定理求得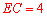 ,证明四边形ABDC是等腰梯形,根据对称性、圆周角定理和垂径定理的综合应用证明
,证明四边形ABDC是等腰梯形,根据对称性、圆周角定理和垂径定理的综合应用证明 ,并由勾股定理列式求角即可.
,并由勾股定理列式求角即可.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
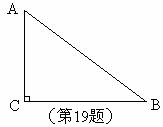
如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等。
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
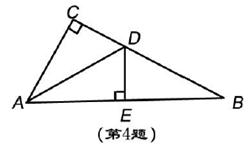
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( ).
A.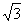 B.2 C.3 D.
B.2 C.3 D.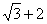
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
把一个长、宽、高分别为3cm、2cm、1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S( )与高
)与高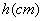 之间的函数关系是为_________________________
之间的函数关系是为_________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
2015年中国高端装备制造业收入将超过6万亿元,其中6万亿元用科学计数法可表示为【 】
A. 0.6×1013元 B. 60×1011元 C. 6×1012元 D. 6×1013元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com