
【题目】如图:已知矩形ABCD中,AB=![]() cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转
cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转![]() 角(
角(![]() ),得到矩形A′B′C′D′
),得到矩形A′B′C′D′
(1)求证:AC⊥OB;
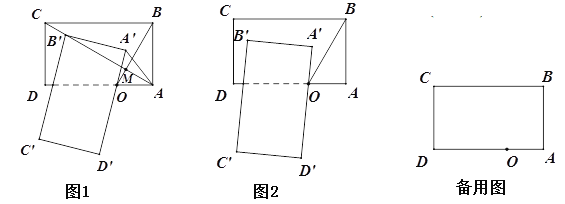
(2)如图1, 当B′落在AC上时,求AA′;
(3)如图2,求旋转过程中△CC′D′的面积的最大值.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由三角函数可求得∠AOB=60°,∠CAD=30°,易证AC⊥OB;
(2)求出OB、BB′,利用![]() 可求得
可求得![]() ;
;
(3)过C点作CH⊥于C′D′点H,连结OC,则CH≤OC+OD′,由此可判断出D′在CO的延长线上时△CC′D′的面积最大,然后根据三角形面积公式求解即可.
解:(1)Rt△OAB中,![]() ∴∠AOB=60°
∴∠AOB=60°
Rt△ACD中,![]()
∴∠CAD=30°
∴∠OMA=180°-60°-30°=90°
即AC⊥OB
(2)Rt△OAM中,![]()
Rt△OAB中,OB′=OB=![]() =2,
=2,
Rt△O B′M中,B′M=![]() ,
,
BM=OB-OM=![]() ,
,
Rt△BB′M中,![]()
![]()
∴![]() ,
,
∴![]()
(3)如图,过C点作CH⊥于C′D′点H,连结OC,则CH≤OC+OD′
只有当D′在CO的延长线上时,CH才最大.
又C′D′长一定,故此时△CC′D′的面积的最大.
而![]()
∴△CC′D′的最大面积为![]()


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
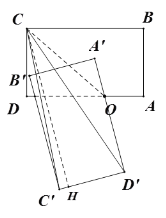
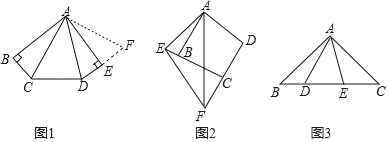
【题目】(1)如图1,在五边形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,试猜想BC,CD,DE之间的数量关系.小明经过仔细思考,得到如下解题思路:
将△ABC绕点A逆时针旋转90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即点D,E,F三点共线,易证△ACD≌ ,故BC,CD,DE之间的数量关系是 ;
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠D=180°,点E,F分别在边CB,DC的延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=2,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
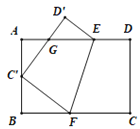
【题目】如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C'处,点D落在点D'处,C'D'交线段AE于点G.
(1)求证:△BC'F∽△AGC';
(2)若C'是AB的中点,AB=6,BC=9,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
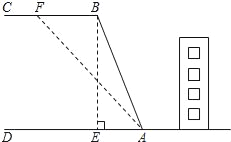
【题目】如图,山区某教学楼后面紧邻着一个土坡,坡面BC平行于地面AD,斜坡AB的坡比为i=1:![]() ,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
,且AB=26米,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,经地质人员勘测,当坡角不超过53°时,可确保山体不滑坡;
(1)求改造前坡顶与地面的距离BE的长;
(2)为了消除安全隐患,学校计划将斜坡AB改造成AF(如图所示),那么BF至少是多少米?(结果精确到1米)
【参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33,cot53°≈0.75】
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,现从中任意摸出一个是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;
(3)若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小明共摸6次小球(每次摸1个球,摸后放回)得20分,问小明有哪几种摸法?
查看答案和解析>>
科目:初中数学 来源: 题型:
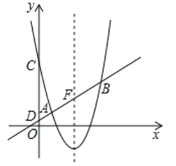
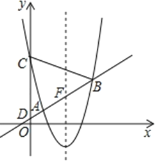
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与直线
与直线![]() 交于A(1,1),B两点,与
交于A(1,1),B两点,与![]() 轴交于点C,直线
轴交于点C,直线![]() 与轴交于点D.
与轴交于点D.
(1)求抛物线的对称轴和点C的坐标;
(2)若在![]() 轴上有且只有一点P,使∠APB=90°,求
轴上有且只有一点P,使∠APB=90°,求![]() 的值;
的值;
(3)设直线![]() 与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若
与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若![]() ,且△BCG与△BCD的面积相等,求点G的坐标.
,且△BCG与△BCD的面积相等,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
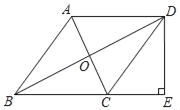
【题目】如图,O为△ABC边AC的中点,AD∥BC交BO的延长线于点D,连接DC,DB平分∠ADC,作DE⊥BC,垂足为E.
(1)求证:四边形ABCD为菱形;
(2)若BD=8,AC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(t,y1),B(t+2,y2)在抛物线![]() 的图象上,且﹣2≤t≤2,则线段AB长的最大值、最小值分别是( )
的图象上,且﹣2≤t≤2,则线段AB长的最大值、最小值分别是( )
A. 2![]() ,2B. 2
,2B. 2![]() ,2
,2![]() C. 2
C. 2![]() ,2D. 2
,2D. 2![]() ,2
,2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com