
【题目】在平面直角坐标系![]() 中,点A
中,点A![]() 是直线
是直线![]() 上一点,点B
上一点,点B![]() 是
是![]() 轴上一点,且AB=6,则△AOB面积的最大值是________.
轴上一点,且AB=6,则△AOB面积的最大值是________.
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
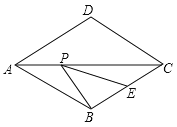
【题目】如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为( )
A. ![]() +1B.
+1B. ![]() C.
C. ![]() +1D.
+1D. ![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,对于P(a,b),若点P'的坐标为(ka+b, ![]() )(其中k为常数且k≠0),则称点P'为点P的“k的和谐点” .已知点A在函数
)(其中k为常数且k≠0),则称点P'为点P的“k的和谐点” .已知点A在函数![]() 的图像上运动,且点A是点B的“
的图像上运动,且点A是点B的“![]() 的和谐点”,若Q(-2, 0),则BQ的最小值为_______.
的和谐点”,若Q(-2, 0),则BQ的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
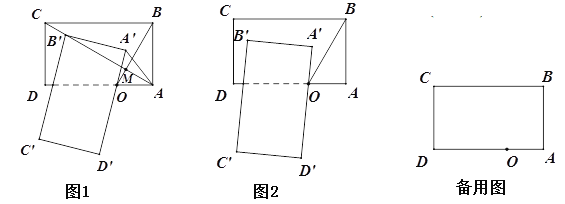
【题目】如图:已知矩形ABCD中,AB=![]() cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转
cm,BC=3cm,点O在边AD上,且AO=1cm.将矩形ABCD绕点O逆时针旋转![]() 角(
角(![]() ),得到矩形A′B′C′D′
),得到矩形A′B′C′D′
(1)求证:AC⊥OB;
(2)如图1, 当B′落在AC上时,求AA′;
(3)如图2,求旋转过程中△CC′D′的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克,经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂生产的B产品不少于38件且不多于40件,若希望用于购买甲、乙两种材料的资金最少,应如何安排生产?最少购买资金是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为30万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破30台.
(1)设当月该型号汽车的销售量为x辆(x≤30,且x为正整数),实际进价为y万元/辆,求y与x的函数关系式;
(2)已知该型号汽车的销售价为32万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?(注:销售利润=销售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
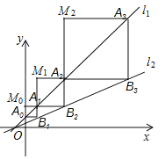
【题目】如图,在平面直角坐标系中,直线l1:y=x+1与y轴交于点A0,过点A0作x轴的平行线交直线l2:y=![]() 点B1,过点B1作y轴的平行线交直线l1于点A1,以A0,B1,A1为顶点构造矩形A0B1A1M0;再过点A1作x轴平行线交直线l2于点B2,过点B2作y轴的平行线交直线l1于点A2,以A1,B2,A2为顶点构造矩形A1B2A2M1;…;照此规律,直至构造矩形AnBn+1An+1Mn,则矩形AnBn+1An+1Mn的周长是_____.
点B1,过点B1作y轴的平行线交直线l1于点A1,以A0,B1,A1为顶点构造矩形A0B1A1M0;再过点A1作x轴平行线交直线l2于点B2,过点B2作y轴的平行线交直线l1于点A2,以A1,B2,A2为顶点构造矩形A1B2A2M1;…;照此规律,直至构造矩形AnBn+1An+1Mn,则矩形AnBn+1An+1Mn的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
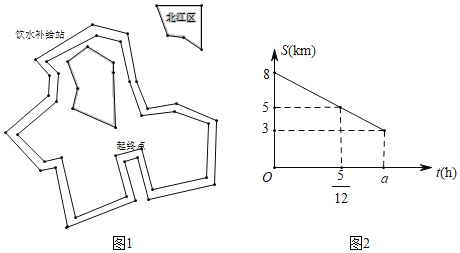
【题目】“2019宁波国际山地马拉松赛”于2019年3月31日在江北区举行,小林参加了环绕湖8km的迷你马拉松项目(如图1),上午8:00起跑,赛道上距离起点5km处会设置饮水补给站,在比赛中,小林匀速前行,他距离终点的路程s(km)与跑步的时间t(h)的函数图象的一部分如图2所示
(1)求小林从起点跑向饮水补给站的过程中与t的函数表达式
(2)求小林跑步的速度,以及图2中a的值
(3)当跑到饮水补给站时,小林觉得自己跑得太悠闲了,他想挑战自己在上午8:55之前跑到终点,那么接下来一段路程他的速度至少应为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com