练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是某斜拉桥引申出的部分平面图，AE，CD是两条拉索，其中拉索CD与水平桥面BE的夹角为72°，其底端与立柱AB底端的距离BD为4米，两条拉索顶端距离AC为2米，若要使拉索AE与水平桥面的夹角为35°，请计算拉索AE的长．（结果精确到0.1米）（参考数据：sin35°≈，cos35°≈，tan35°≈，sin72°≈，cos72°≈，tan72°≈）

    【答案】拉索AE的长为26.2m．

    【解析】

    利用锐角三角函数关系得出AB的长，进而得出AE的长即可得出答案．

    解：由题意可得：tan72°===，

    解得：BC=，

    则AB=BC+AC=+2＝（m），

    故sin35°===，

    解得：AE≈26.2，

    答：拉索AE的长为26.2m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线与轴交于点与轴交于点二次函数的图象经过两点，且与轴的负半轴交于点．

    求二次函数的解析式及点的坐标．

    点是线段上的一动点，动点在直线下方的二次函数图象上．设点的横坐标为．过点作于点求线段的长关于的函数解析式，并求线段的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知矩形ABCD中，BC＝2AB，点E在BC边上，连接DE、AE，若EA平分∠BED，则的值为（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以为顶点的抛物线交轴于点，，交轴于点．

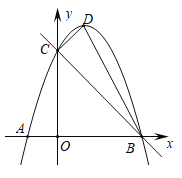
    （1）求抛物线的解析式；

    （2）在直线上有一点，使的值最小，求点的坐标；

    （3）在轴上是否存在一点，使得以，，为顶点的三角形与相似？若存在，请求出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形ABCD中，AB＝2，AD＝4，将矩形ABCD绕点C顺时针旋转至矩形EGCF（其中E、G、F分别与A、B、D对应）．

    （1）如图1，当点G落在AD边上时，直接写出AG的长为　 　；

    （2）如图2，当点G落在线段AE上时，AD与CG交于点H，求GH的长；

    （3）如图3，记O为矩形ABCD对角线的交点，S为△OGE的面积，求S的取值范围．

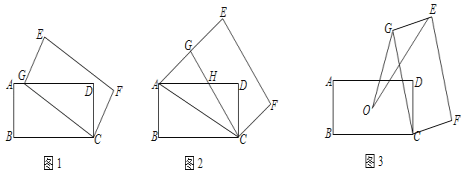
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，学生会随机抽取了20名七、八年级学生（每个年级各10人）进行问卷调查，并把他们的得分绘制成了如下表格，计分采用10分制（得分均取整数）成绩达到6分或6分以上为及格，达到9分及以上为优秀，成绩如表1所示，并制作了成绩分析表（表2）．

    表1

    七年级

    5

    8

    8

    8

    10

    10

    8

    5

    5

    八年级

    10

    6

    6

    9

    4

    5

    7

    10

    8

    表2

    年级

    平均数

    中位数

    众数

    方差

    及格率

    优秀率

    七年级

    7.6

    8

    8

    3.82

    70%

    八年级

    7.5

    10

    4.94

    80%

    40%

    （1）在表1中，_____，_____；在表2中，_____，______；

    （2）根据表2成绩数据分析，你认为哪个年级的学生对垃圾分类了解更加深入，请说明你的理由；

    （3）小明根据表2数据作出如下判断：

    ①七年级学生成绩的平均数高于八年级，故七年级学生一定比八年级学生优秀；

    ②被调查对象中，七年级学生的成绩更加稳定；

    ③学校七年级和八年级共有400人，估计有280人成绩达到优秀；

    ④七年级不及格人数比八年级多；

    对小明的四个结论，随机任选两个，求都是错误的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD中，对角线AC、BD交于O点，DE∥AC，CE∥BD．

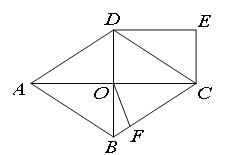
    （1）求证：四边形OCED为矩形；

    （2）在BC上截取CF＝CO，连接OF，若AC＝16，BD＝12，求四边形OFCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车交易市场为了解二手轿车的交易情况，将本市场去年成交的二手轿车的全部数据，以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类，并根据这些数据由甲，乙两人分别绘制了下面的两幅统计图（图都不完整）．

    请根据以上信息，解答下列问题：

    （1）该汽车交易市场去年共交易二手轿车　 　辆．

    （2）把这幅条形统计图补充完整．（画图后请标注相应的数据）

    （3）在扇形统计图中，D类二手轿车交易辆数所对应扇形的圆心角为　 　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，抛物线y＝x2+bx+c与x轴交于A、B两点，与y轴交于点C，对称轴为直线x＝2，点A的坐标为（1，0）．

    （1）求该抛物线的表达式及顶点坐标；

    （2）点P为抛物线上一点（不与点A重合），连接PC．当∠PCB＝∠ACB时，求点P的坐标；

    （3）在（2）的条件下，将抛物线沿平行于y轴的方向向下平移，平移后的抛物线的顶点为点D，点P的对应点为点Q，当OD⊥DQ时，求抛物线平移的距离．

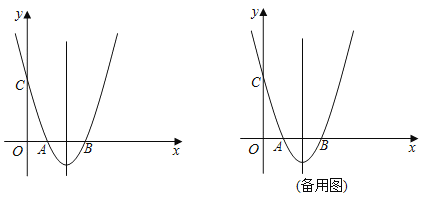
    查看答案和解析>>

    同步练习册答案