
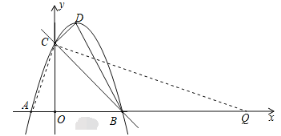
【题目】如图,以![]() 为顶点的抛物线
为顶点的抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() ,交
,交![]() 轴于点
轴于点![]() .
.
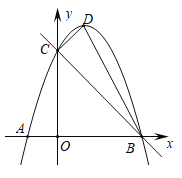
(1)求抛物线的解析式;
(2)在直线![]() 上有一点
上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为![]() ;(3)存在,当
;(3)存在,当![]() 的坐标为
的坐标为![]() 或
或![]() 时,以
时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【解析】
(1)将点B和点C的坐标代入二次函数解析式中即可求出结论;
(2)先求出点A的坐标,利用待定系数法求出BC的解析式,作点O关于BC的对称点O′,连接AO′交BC于点P,连接OP,O′B,根据两点之间线段最短,此时![]() 最小,求出点O′的坐标,利用待定系数法求出AO′的解析式,联立方程即可求出结论;
最小,求出点O′的坐标,利用待定系数法求出AO′的解析式,联立方程即可求出结论;
(3)求出顶点D的坐标,利用平面直角坐标系中任意两点之间的距离公式求出CD、BC、CD和AC,根据勾股定理的逆定理证出△BCD是直角三角形,然后根据相似三角形的对应情况分类讨论,根据相似三角形的性质列出比例式即可求出结论.
解:(1)将点B和点C的坐标代入![]() 中,得
中,得
![]()
解得: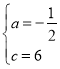
∴抛物线的解析式为![]() ;
;
(2)把y=0代入![]() 中,得
中,得
![]()
解得:x1=-2,x2=6,
∴点A的坐标为(-2,0)
设直线BC的解析式为y=kx+b
将点B和点C的坐标代入,得
![]()
解得:![]()
∴直线BC的解析式为![]()
作点O关于BC的对称点O′,连接AO′交BC于点P,连接OP,O′B
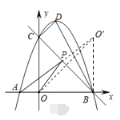
根据对称可得PO=PO′,OB=O′B
此时![]() =
=![]() =
=![]()
根据两点之间线段最短,此时![]() 最小
最小
∵OB=OC=6,∠BOC=90°
∴∠OBC=45°
∴∠OBO′=90°
∵OB= O′B =6
∴点O′的坐标为(6,6)
设直线AO′的解析式为y=mx+n
将点A和点O′的坐标代入,得
![]()
解得: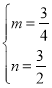
∴直线AO′的解析式为![]()
联立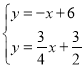
解得: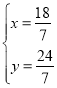
∴点P的坐标为![]()
(3)∵![]() =
=![]()
∴点D的坐标为(2,8)
∴![]()
![]()
∴CD2+BC2=80=BD2
∴△BCD为直角三角形,且∠BCD=90°
点Q在点A左侧时,△QAC为钝角三角形,
∴△QAC不可能与△BCD相似
∴点Q必在点A右侧,设点Q的坐标为(q,0),则AQ=q-(-2)=q+2
∵tan∠CAO=![]() ,tan∠BDC=
,tan∠BDC=![]()
∴∠CAO=∠BDC
当△CQA∽△BCD时,
∴![]()
即![]()
解得:q=0
∴点Q的坐标为(0,0);
当△QCA∽△BCD时,
∴![]()
即![]()
解得:q=18
∴点Q的坐标为(18,0);
综上:点Q的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】在一次数学测验中,八年级(1)班的成绩如下表:
分数 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
人数 | 2 | 3 | 10 | 6 | 4 | 7 | 6 | 2 |
(1)本次数学测验成绩的平均数,中位数,众数各是多少?
(2)若老师把人数中的数据“10”看成了“9”,数据“7”看成了“8”,则平均数,中位数,众数中不受影响的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
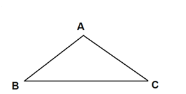
【题目】如图,在△ABC中,AB=AC.
(1)若以点A为圆心的圆与边BC相切于点D,请在下图中作出点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若该圆与边AC相交于点E,连接DE,当∠BAC=100°时,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△EBC中,∠B=90°,A为BE边上一点,以边AC上的点O为圆心、OA为半径的圆O与EC相切,D为切点,AD∥BC.
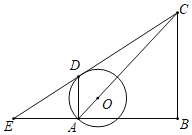
(1)求证:∠E=∠ACB.
(2)若AD=1,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,将
上,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() 处,又将
处,又将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在直线
落在直线![]() 与
与![]() 的交点
的交点![]() 处.
处.
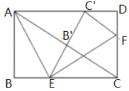
(1)求证:点![]() 在
在![]() 的角平分线上;
的角平分线上;
(2)求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
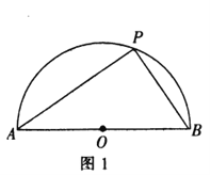
【题目】[问题发现]如图1,半圆![]() 的直径
的直径![]() 是半圆
是半圆![]() 上的一个动点,则
上的一个动点,则![]() 面积的最大值是_.
面积的最大值是_.
[问题解决]如图2所示的是某街心花园的一角.在扇形![]() 中,
中,![]() 米,在围墙
米,在围墙![]() 和
和![]() 上分别有两个入口
上分别有两个入口![]() 和
和![]() 且
且![]() 米,
米,![]() 是
是![]() 的中点,出口
的中点,出口![]() 在
在![]() 上.现准备沿
上.现准备沿![]() 从入口到出口铺设两条景观小路,在四边形
从入口到出口铺设两条景观小路,在四边形![]() 内种花,在剩余区域种草.
内种花,在剩余区域种草.
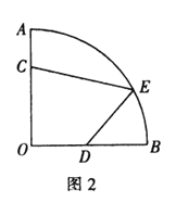
①出口![]() 设在距直线
设在距直线![]() 多远处可以使四边形
多远处可以使四边形![]() 的面积最大?最大面积是多少?(小路宽度不计)
的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路![]() 所用的普通石材每米的造价是
所用的普通石材每米的造价是![]() 元,铺设小路
元,铺设小路![]() 所用的景观石材每米的造价是
所用的景观石材每米的造价是![]() 元问:在
元问:在![]() 上是否存在点
上是否存在点![]() ,使铺设小路
,使铺设小路![]() 和
和![]() 的总造价最低?若存在,请求出最低总造价和出口
的总造价最低?若存在,请求出最低总造价和出口![]() 距直线
距直线![]() 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某斜拉桥引申出的部分平面图,AE,CD是两条拉索,其中拉索CD与水平桥面BE的夹角为72°,其底端与立柱AB底端的距离BD为4米,两条拉索顶端距离AC为2米,若要使拉索AE与水平桥面的夹角为35°,请计算拉索AE的长.(结果精确到0.1米)(参考数据:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,sin72°≈
,sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°≈
,tan72°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
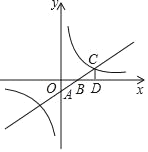
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴于D,若OB=3,OD=6,△AOB的面积为3.
(1)求一次函数与反比例函数的表达式;
(2)当x>0时,比较kx+b与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com