
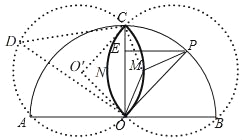
【题目】如图,AB为⊙O的直径,且AB=4,点C在半圆上,OC⊥AB,垂足为点O,P为半圆上任意一点,过P点作PE⊥OC于点E,设△OPE的内心为M,连接OM、PM.当点P在半圆上从点B运动到点A时,内心M所经过的路径长为_____.

【答案】![]()
【解析】
根据三角形内心的性质可求得∠PMO=135°,再由全等三角形的判定和性质可得∠CMO=135°,过C、M、O三点作⊙O′,连O′C,O′O,在优弧CO取点D,连DC,DO,在等腰直接三角形中求得O′O,从而求得弧OMC,同理可求得弧ONC,从而求得点M所经过的路径.
解:∵△OPE的内心为M,
∴∠MOP=∠MOC,∠MPO=∠MPE,
∴∠PMO=180°﹣∠MPO﹣∠MOP=180°﹣![]() (∠EOP+∠OPE),
(∠EOP+∠OPE),
∵PE⊥OC,即∠PEO=90°,
∴∠PMO=180°﹣![]() ×(∠EOP+∠OPE)=180°﹣
×(∠EOP+∠OPE)=180°﹣![]() ×(180°﹣90°)=135°,
×(180°﹣90°)=135°,
如图,连接OC,
∵OP=OC,OM=OM,
而∠MOP=∠MOC,
∴△OPM≌△OCM(SAS),
∴∠CMO=∠PMO=135°,
所以点M在以OC为弦,并且所对的圆周角为135°的两段劣弧上(弧OMC和弧ONC);
点M在扇形BOC内时,
过C、M、O三点作⊙O′,连O′C,O′O,
在优弧CO取点D,连DC,DO,
∵∠CMO=135°,
∴∠CDO=180°﹣135°=45°,
∴∠CO′O=90°,而OA=2cm,
∴O′O=![]() OC=
OC=![]() ×2=
×2=![]() ,
,
∴弧OMC的长=![]() cm,
cm,
同理:点M在扇形AOC内时,同①的方法得,弧ONC的长为![]() cm,
cm,
所以内心M所经过的路径长为2×![]() =
=![]() πcm.
πcm.
故答案为:![]() πcm.
πcm.


科目:初中数学 来源: 题型:
【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
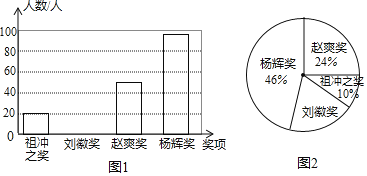
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小明研究了这样一个问题:求使得等式![]() 成立的x的个数.小明发现,先将该等式转化为
成立的x的个数.小明发现,先将该等式转化为![]() ,再通过研究函数
,再通过研究函数![]() 的图象与函数
的图象与函数![]() 的图象(如图)的交点,使问题得到解决.
的图象(如图)的交点,使问题得到解决.
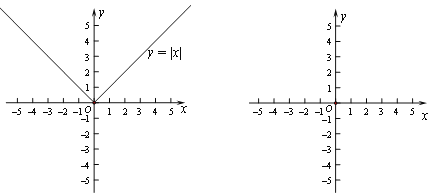
(1)当k=1时,使得原等式成立的x的个数为_______;
(2)当0<k<1时,使得原等式成立的x的个数为_______;
(3)当k>1时,使得原等式成立的x的个数为_______.
参考小明思考问题的方法,解决问题:关于x的不等式![]() 只有一个整数解,求
只有一个整数解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的函数表达式;
求抛物线的函数表达式;
![]() 求抛物线的顶点坐标,直接写出当
求抛物线的顶点坐标,直接写出当![]() 时,x的取值范围;
时,x的取值范围;
![]() 设点M是抛物线的顶点,试判断抛物线上是否存在点H满足
设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
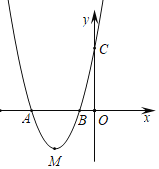
查看答案和解析>>
科目:初中数学 来源: 题型:
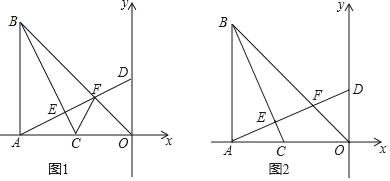
【题目】如图,在Rt△ABO中,∠BAO=90°,AO=AB,BO=8![]() ,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
,点A的坐标(﹣8,0),点C在线段AO上以每秒2个单位长度的速度由A向O运动,运动时间为t秒,连接BC,过点A作AD⊥BC,垂足为点E,分别交BO于点F,交y轴于点 D.
(1)用t表示点D的坐标 ;
(2)如图1,连接CF,当t=2时,求证:∠FCO=∠BCA;
(3)如图2,当BC平分∠ABO时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
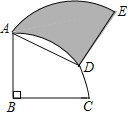
【题目】如图,将半径为4,圆心角为90°的扇形BAC绕A点逆时针旋转60°,点B、C的对应点分别为点D、E且点D刚好在![]() 上,则阴影部分的面积为_____.
上,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:

请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com