
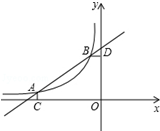
 如图,已知A(-4,$\frac{1}{2}$),B(-1,a)是一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,$\frac{1}{2}$),B(-1,a)是一次函数y=$\frac{1}{2}$x+b与反比例函数y=$\frac{m}{x}$(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.分析 (1)根据反比例函数图象上点的坐标特征可计算出m=-4×$\frac{1}{2}$=-2,再把B(-1,a)代入y=-$\frac{2}{x}$可求得a=2,然后把A点坐标代入y=$\frac{1}{2}$x+b求出b,从而得到一次函数解析式;
(2)连接PC、PD,如图,设P(x,$\frac{1}{2}$x+$\frac{5}{2}$),根据三角形面积公式得到$\frac{1}{2}$×$\frac{1}{2}$×(x+4)=$\frac{1}{2}$×|-1|×(2-$\frac{1}{2}$x-$\frac{5}{2}$),解得x=$\frac{5}{2}$,然后计算自变量为$\frac{5}{2}$时的一次函数值即可得到P点坐标.
解答 解:(1)∵反比例y=$\frac{m}{x}$的图象过点(-4,$\frac{1}{2}$),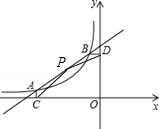
∴m=-4×$\frac{1}{2}$=-2,
把B(-1,a)代入y=-$\frac{2}{x}$得-a=-2,解得a=2,
∵y=$\frac{1}{2}$x+b的图象过点A(-4,$\frac{1}{2}$)
∴$\frac{1}{2}$×(-4)+b=$\frac{1}{2}$,解得b=$\frac{5}{2}$,
∴一次函数的表达式是y=$\frac{1}{2}$x+$\frac{5}{2}$;
(2)连接PC、PD,如图,设P(x,$\frac{1}{2}$x+$\frac{5}{2}$),
∵△PCA和△PDB面积相等,
∴$\frac{1}{2}$×$\frac{1}{2}$×(x+4)=$\frac{1}{2}$×|-1|×(2-$\frac{1}{2}$x-$\frac{5}{2}$),解得x=$\frac{5}{2}$,
当x=$\frac{5}{2}$时,y=$\frac{1}{2}$x+$\frac{5}{2}$=$\frac{5}{4}$,
∴P点坐标是(-$\frac{5}{2}$,$\frac{5}{4}$).
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.注意用点的坐标表示线段的长.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有5次正面朝上 | B. | 不可能10次正面朝上 | ||
| C. | 不可能10次正面朝下 | D. | 可能有5次正面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
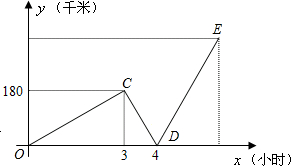 快、慢两车同时从A地出发沿同一线路匀速驶往B地,快车到达B地后立即按原路原速返回A地,慢车不返回,两车之间的路程y(千米)与行驶时间x(小时)的函数关系图象如图所示,请你解答下列问题:
快、慢两车同时从A地出发沿同一线路匀速驶往B地,快车到达B地后立即按原路原速返回A地,慢车不返回,两车之间的路程y(千米)与行驶时间x(小时)的函数关系图象如图所示,请你解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.
如图,点E是矩形ABCD的边AB上一点,将△BEC沿CE折叠,使点B落在AD边上的点F处.若△AEF∽△FEC∽△DFC,则$\frac{AB}{BC}$的值是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com