
分析 直接利用三角形的形状可分为锐角三角形和钝角三角形,分别利用勾股定理求出BD,DC的长,进而得出BC的长.
解答 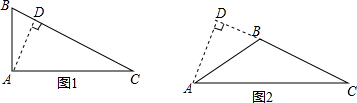 解:如图1,过点A作AD⊥BC于点D,
解:如图1,过点A作AD⊥BC于点D,
∵AC=8,∠ACB=30°,
∴AD=4,
∴DC=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴BD=$\sqrt{(\sqrt{19})^{2}-{4}^{2}}$=$\sqrt{3}$,
∴BC=DC+BD=5$\sqrt{3}$;
如图2,过点A作AD⊥CB延长线与点D,
同理可得:AD=4,DC=4$\sqrt{3}$,DB=$\sqrt{3}$,
则BC=3$\sqrt{3}$,
综上所述:BC的长为5$\sqrt{3}$或3$\sqrt{3}$.
点评 此题主要考查了勾股定理以及直角三角的性质,根据题意分类讨论求出是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
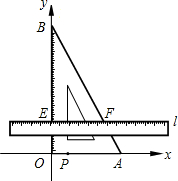 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com