
【题目】如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN. 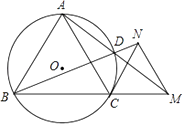
(1)判断△CMN的形状,并证明你的结论;
(2)求证:CN是⊙O的切线;
(3)若等边△ABC的边长是2,求ADAM的值.
【答案】
(1)解:△CMN为等边三角形.理由如下:
∵△ABC为等边三角形,
∴CB=CA,∠ABC=∠ACB=60°,
在△BCN和△ACM中
 ,
,
∴△BCN≌△ACM,
∴CN=CM,∠BCN=∠ACM,
∴∠ACB+∠ACN=∠ACN+∠MCN,
∴∠MCN=∠ACB=60°,
∴△CMN为等边三角形
(2)证明:连接OC,如图,
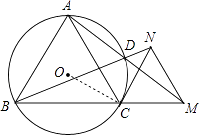
∵CA=CB,
∴ ![]() =
= ![]() ,
,
∴OC⊥AB,
∵∠ABC=∠MCN=60°,
∴AB∥CN,
∴OC⊥CN,
∴CN是⊙O的切线
(3)解:连接CD,如图,
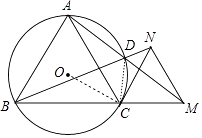
∵∠ADC+∠ABC=180°,∠ACM+∠ACB=180°,
而∠ABC=∠ACB=60°,
∴∠ADC=∠ACM,
而∠DAC=∠CAM,
∴△ACD∽△AMC,
∴AC:AD=AM:AC,
∴ADAM=AC2,
∵等边△ABC的边长是2,
∴AC=2,
∴ADDM=4.
【解析】(1)利用等边三角形的性质得到CB=CA,∠ABC=∠ACB=60°,再证明△BCN≌△ACM得到CN=CM,∠BCN=∠ACM,则∠MCN=∠ACB=60°,于是可判断△CMN为等边三角形;(2)连接OC,如图,利用CA=CB得到 ![]() =
= ![]() ,则根据垂径定理的推论得到OC⊥AB,再证明AB∥CN,则OC⊥CN,然后根据切线的判定方法可判断CN是⊙O的切线;(3)连接CD,如图,证明△ACD∽△AMC,利用相似比得到ADAM=AC2 , 然后利用等边△ABC的边长是2可得到ADDM的值.
,则根据垂径定理的推论得到OC⊥AB,再证明AB∥CN,则OC⊥CN,然后根据切线的判定方法可判断CN是⊙O的切线;(3)连接CD,如图,证明△ACD∽△AMC,利用相似比得到ADAM=AC2 , 然后利用等边△ABC的边长是2可得到ADDM的值.


科目:初中数学 来源: 题型:
【题目】如图,直线y=x+1与y轴交于点A1 , 依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、…,An在直线x+1上,点C1、C2、…,Cn在x轴上,则点Bn的坐标是( )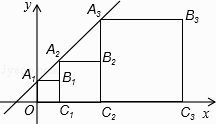
A.(2n﹣1,2n﹣1)
B.(2n﹣1+1,2n﹣1)
C.(2n﹣1,2n﹣1)
D.(2n﹣1,n)
查看答案和解析>>
科目:初中数学 来源: 题型:
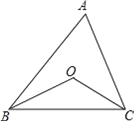
【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
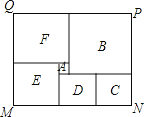
【题目】如图长方形MNPQ是菜市民健身广场的平面示意图,它是由6个正方形拼成的长方形,中间最小的正方形A的边长是1,观察图形特点可知长方形相对的两边是相等的(如图中MN=PQ).正方形四边相等.请根据这个等量关系,试计算长方形MNPQ的面积,结果为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1 cm,△ACD的周长为12 cm,则△ABC的周长是( )
![]()
A. 13 cm B. 14 cm C. 15 cm D. 16 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班有48名学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去动物园的学生数”的扇形圆心角为60°,则下列说法正确的是( )
A. 想去动物园的学生占全班学生的60% B. 想去动物园的学生有12人
C. 想去动物园的学生肯定最多 D. 想去动物园的学生占全班学生的![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1 , △OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2 , 记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3 , 记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016 , 记抛物线y2016与x轴的另一交点为A2016 , 顶点为P2016 . 若这2016条抛物线的顶点都在射线OP1上.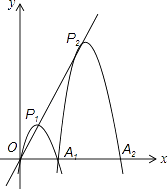
(1)①求△OP1A1的面积;②求a,b的值;
(2)求抛物线y2的解析式;
(3)请直接写出点A2016以及点P2016坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
R三点分别在CD、AD、BC上,如图所示.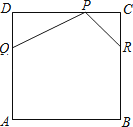
(1)当皮雕师傅切下△PDQ时,若DQ长度为x公分,请你以x表示此时△PDQ的面积.
(2)承(1),当x的值为多少时,五边形PQABR的面积最大?请完整说明你的理由并求出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com