练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠A＝90°，AB＝3，AC＝4，D为AC中点，P为AB上的动点，将P绕点D逆时针旋转90°得到P′，连CP′的最小值为（　　）

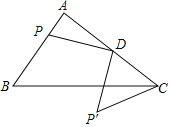
    A.1.6B.2.4C.2D.2

    【答案】C

    【解析】

    先过P'作P'E⊥AC于E，根据△DAP≌△P'ED，可得P'E=AD=2，再根据当AP=DE=2时，DE=DC，即点E与点C重合，即可得出线段CP′的最小值为2．

    如图，过点P′作P′E⊥AC于点E，

    则∠A＝∠P′ED＝90°，

    由旋转可知：

    DP＝DP′，∠PDP′＝90°，

    ∴∠ADP＝∠EP′D，

    ∴△DAP≌△P′ED（AAS）

    ∴P′E＝AD＝2，

    ∴当AP＝DE＝2时，DE＝DC，即点E与点C重合，

    此时CP′＝EP′＝2

    ∴线段CP′的最小值为2．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

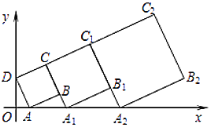
    【题目】在平面坐标系中，正方形的位置如图所示，点的坐标为，点的坐标为，延长交轴于点，作正方形，正方形的面积为______，延长交轴于点，作正方形，……按这样的规律进行下去，正方形的面积为______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

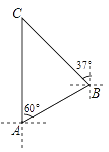
    【题目】知识改变世界，科技改变生活.导航装备的不断更新极大方便了人们的出行.如图，某校组织学生乘车到黑龙滩（用C表示）开展社会实践活动，车到达A地后，发现C地恰好在A地的正北方向，且距离A地13千米，导航显示车辆应沿北偏东60°方向行驶至B地，再沿北偏西37°方向行驶一段距离才能到达C地，求B、C两地的距离.（参考数据：sin53°≈,cos53°≈，tan53°≈)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y＝﹣x+1与x轴，y轴分别交于A，B两点，抛物线y＝ax2+bx+c过点B，并且顶点D的坐标为（﹣2，﹣1）．

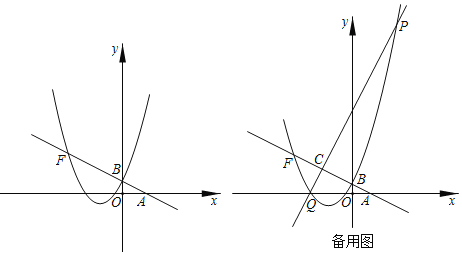
    （1）求该抛物线的解析式；

    （2）若抛物线与直线AB的另一个交点为F，点C是线段BF的中点，过点C作BF的垂线交抛物线于点P，Q，求线段PQ的长度；

    （3）在（2）的条件下，点M是直线AB上一点，点N是线段PQ的中点，若PQ＝2MN，直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个四位数，记千位数字与个位数字之和为，十位数字与百位数字之和为，如果，那么称这个四位数为“对称数”

    最小的“对称数”为 ；四位数与之和为最大的“对称数”，则的值为 ；

    一个四位的“对称数”，它的百位数字是千位数字的倍，个位数字与十位数字之和为，且千位数字使得不等式组恰有个整数解，求出所有满足条件的“对称数”的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

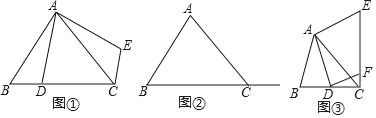
    【题目】（1）观察猜想：

    在Rt△ABC中，∠BAC=90°，AB=AC，点D在边BC上，连接AD，把△ABD绕点A逆时针旋转90°，点D落在点E处，如图①所示，则线段CE和线段BD的数量关系是　 　，位置关系是　 　．

    （2）探究证明：

    在（1）的条件下，若点D在线段BC的延长线上，请判断（1）中结论是还成立吗？请在图②中画出图形，并证明你的判断．

    （3）拓展延伸：

    如图③，∠BAC≠90°，若AB≠AC，∠ACB=45°，AC=，其他条件不变，过点D作DF⊥AD交CE于点F，请直接写出线段CF长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

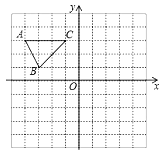
    【题目】如图,网格中已知△ABC三个顶点的坐标分别为(-4,3)、(-3,1)、(-1,3)，按要求解决下列问题：

    (1)将△ABC向右平移1个单位长度，再向下平移4个单位长度，得到，作出；

    (2)将绕点O逆时针旋转90°，得到作出

    查看答案和解析>>

    科目：初中数学 来源： 题型：

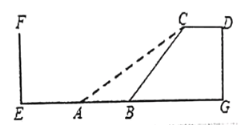
    【题目】速滑运动受到许多年轻人的喜爱。如图，四边形是某速滑场馆建造的滑台，已知，滑台的高为米，且坡面的坡度为.后来为了提高安全性，决定降低坡度，改造后的新坡面AC的坡度为.

    （1）求新坡面的坡角及的长；

    （2）原坡面底部的正前方米处是护墙，为保证安全，体育管理部门规定，坡面底部至少距护墙米。请问新的设计方案能否通过，试说明理由（参考数据：）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

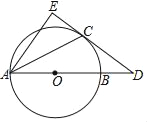
    【题目】如图，点D在⊙O的直径AB的延长线上，CD切⊙O于点C，AE⊥CD于点E

    （1）求证：AC平分∠DAE；

    （2）若AB＝6，BD＝2，求CE的长．

    查看答案和解析>>

    同步练习册答案