
【题目】如图,![]() 中,
中,![]() ,则
,则![]() ____.
____.
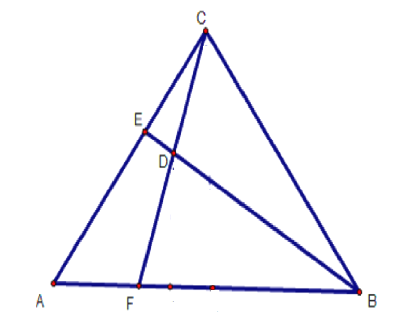
【答案】2![]()
【解析】
如下图,先推导出∠DFB=60°,并得出△ECD∽△FBD,设FG=a,则利用相似,可得出FB的大小,从而得出GB的长,然后再Rt△DGB中,得出DB的长,从而得出CB的长,最后在Rt△CHB中,利用勾股定理求出a的值,进而得出AF的长.
如下图,过点D、C作AB的垂线,分别交AB于点G、H
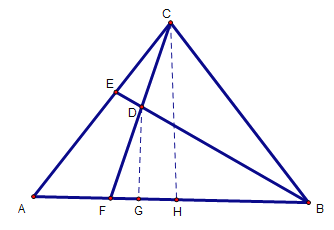
∵BD=BC=AC,∴∠CDB=∠DCB
∵∠ACB+∠CBD=120°,∠CDB+∠DCB+∠CBD=180°
∴∠ACF+∠DCB+∠CBD=120°
∴∠CDB=∠ACF+60°
设∠ACF=x,则∠DCB=∠CDB=x+60
∴∠CAB=∠CBA=60-x,∠CBE=60-2x,∠EBA=x
∴∠CFB=∠ACF+∠CAF=60°
∵∠ECD=∠DBF=x,∠CDE=∠BDF
∴△ECD∽△FBD
设FG=a
则在Rt△FGD中,FD=2a,DG=![]()
∵△ECD∽△FBD,CE=3,ED=1
∴![]()
解得:FB=6a
∴GB=5a
∴在Rt△DBG中,DB=2![]() a=BC
a=BC
∵![]()
∴CD=2![]()
∴在Rt△CFH中,FH=![]() ,CH=
,CH=![]()
∴GH=![]() ,HB=5a-
,HB=5a-![]()
∵AC=BC
∴AH=BH=5a-![]()
∴AF=AH-FG-GH=5a-![]() =4a-2
=4a-2![]()
在Rt△CHB中,![]() ,即
,即![]()
解得;a=![]()
∴AF=4a-2![]() =4
=4![]()
故答案为:2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某水果连锁店销售某种热带水果,其进价为20元/千克.销售一段时间后发现:该水果的日销量![]() (千克)与售价
(千克)与售价![]() (元/千克)的函数关系如图所示:
(元/千克)的函数关系如图所示:
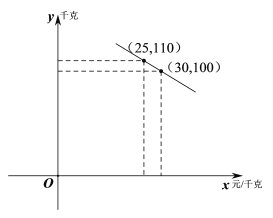
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当售价为多少元/千克时,当日销售利润最大,最大利润为多少元?
(3)由于某种原因,该水果进价提高了![]() 元/千克(
元/千克(![]() ),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是
),物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价仍然满足(1)中的函数关系.若日销售最大利润是![]() 元,请直接写出
元,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,BM,DN分别平分∠ABC,∠CDA,沿BP折叠,点A恰好落在BM上的点E处,延长PE交DN于点F沿DQ折叠,点C恰好落在DN上的点G处,延长QG交BM于点H,若四边形EFGH恰好是正方形,且边长为1,则矩形ABCD的面积为____.
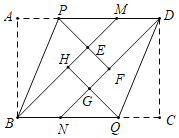
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大数学家欧拉非常推崇观察能力,他说过,今天已知的许多数的性质,大部分是通过观察发现的,历史上许多大家,都是天才的观察家,化归就是将面临的新问题转化为已经熟悉的规范问题的数学方法,这是一种具有普遍适用性的数学思想方法.如多项式除以多项式可以类比于多位数的除法进行计算:
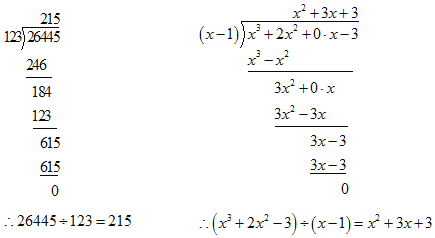
请用以上方法解决下列问题:
(1)计算:(x3+2x2﹣3x﹣10)÷(x﹣2);
(2)若关于x的多项式2x4+5x3+ax2+b能被二项式x+2整除,且a,b均为自然数,求满足以上条件的a,b的值及相应的商.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com