
【题目】如图![]() ,
,![]() 是两条笔直的公路,点
是两条笔直的公路,点![]() 是
是![]() 上的一个超市,现在想建一个服务区
上的一个超市,现在想建一个服务区![]() ,要求到两条公路的距离相等,且服务区到超市
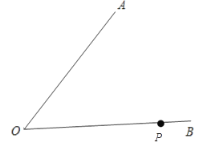
,要求到两条公路的距离相等,且服务区到超市![]() 的距离最近,求作这个服务区.
的距离最近,求作这个服务区.
【答案】图见解析
【解析】
根据角平分线的判定,可知该服务区在∠O的平分线上,再根据垂线段最短,可知点P和服务区的连线垂直于∠O的平分线,故作出∠O的平分线,然后过点P作∠O的平分线的垂线,垂足即为所求.
解:以O为圆心,任意长度为半径作弧,分别交OA、OB于点D、E,分别以D、E为圆心,大于![]() DE的长为半径作弧,两弧交于点F,连接OF并延长,射线OF即为∠AOB的角平分线;
DE的长为半径作弧,两弧交于点F,连接OF并延长,射线OF即为∠AOB的角平分线;
以P为圆心,大于P到OF的距离为半径作弧,交射线OF于G、H,分别以G、H为圆心,大于![]() GH的长为半径作弧,两弧在射线OF上方交于点M,连接PM,与射线OF的交点即为服务区,此时PM⊥OF.
GH的长为半径作弧,两弧在射线OF上方交于点M,连接PM,与射线OF的交点即为服务区,此时PM⊥OF.
根据角平分线的判定和垂线段最短,这个服务区即为所求.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
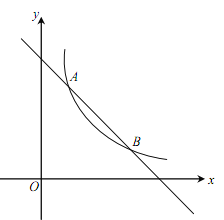
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,把
,把![]() 的各边进行下列变换:①各边的长度分别扩大为原来的3倍;②各边的长度分别缩小为原来的
的各边进行下列变换:①各边的长度分别扩大为原来的3倍;②各边的长度分别缩小为原来的![]() ;③各边的长度分别增加2;④各边的长度分别平方.其中得到的三角形与
;③各边的长度分别增加2;④各边的长度分别平方.其中得到的三角形与![]() 相似的有( )
相似的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
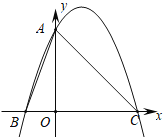
【题目】如图,对称轴为直线x=1的抛物线与x轴交于B、C两点,与y轴交于点A(0,3),且OA=OC.
(1)求抛物线的解析式;
(2)点P是直线AC上方抛物线上的一点,过点P作PD⊥x轴于点D.若△PDC与△AOB相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶被称为“马路第一杀手”为了让驾驶员自觉遵守交通规则,湖浔大道公路检测中心在一事故多发地段安装了一个测速仪器,如图所示,已知检测点设在距离公路10米的A处,测得一辆汽车从B处行驶到C处所用时间为1.35秒.已知∠B=45°,∠C=30°.
(1)求B,C之间的距离(结果保留根号);
(2)如果此地限速为70km/h,那么这辆汽车是否超速?请说明理由.(参考数据;![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 和直线
和直线![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]() 可用公式
可用公式![]() 计算.
计算.
例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:因为直线![]() ,其中
,其中![]() .
.
所以点![]() 到直线
到直线![]() 的距离为
的距离为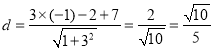 .
.
根据以上材料,解答下列问题:
(1)点![]() 到直线
到直线![]() 的距离;
的距离;
(2)已知![]() 的圆心
的圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() 为2,判断
为2,判断![]() 与直线
与直线![]() 的位置关系并说明理由;
的位置关系并说明理由;
(3)已知直线![]() 与
与![]() 平行,
平行,![]() 、
、![]() 是直线
是直线![]() 上的两点且
上的两点且![]() ,
,![]() 是直线
是直线![]() 上任意一点,求
上任意一点,求![]() 的面积.
的面积.
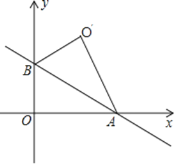
(4)如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,把
两点,把![]() 沿直线
沿直线![]() 翻折后得到
翻折后得到![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
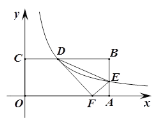
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B 的坐标为(8,4),反比例函数y=![]() (k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
(k>0)的图象分别交边BC、AB 于点D、E,连结DE,△DEF与△DEB关于直线DE对称,当点F恰好落在线段OA上时,则k的值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
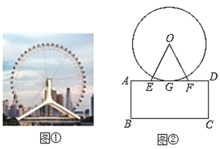
【题目】如图①是长春新地标一一摩天活力城楼顶上的摩天轮,被誉为“长春眼”,如图②是其正面的平面图.已知摩天活力城楼顶AD距地面BC为34米,摩天轮⊙O与楼顶AD近似相切,切点为G.测得∠OEF=∠OFE=67°,EF=27.54米,求摩天轮的最高点到地面BC的距离.(结果精确到0.1米)(参考数据:sin67°=0.92,cos67°0.39,tan67°=2.36)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com