
【题目】如图,菱形 ABCD 中,∠ABC=60°,有一度数为 60°的∠MAN 绕点 A 旋转.
(1)如图①,若∠MAN 的两边 AM、AN 分别交 BC、CD 于点 E、F,则线段 CE、DF的大小关系如何?请证明你的结论.
(2)如图②,若∠MAN 的两边 AM、AN 分别交 BC、CD 的延长线于点 E、F,则线段CE、DF 还有(1)中的结论吗?请说明你的理由.

【答案】(1)CE=DF,证明见解析;(2)仍然有CE=DF,理由见解析.
【解析】
(1)CE=DF;连接AC,易得△ABC、△ACD为正三角形,再根据等边三角形的性质,利用ASA可判定△AEC≌△AFD,即得CE=DF;
(2)结论CE=DF仍然成立,同(1)类似证明△ACE≌△ADF,即得结论.
解:(1))CE=DF;
证明:如图③,连接AC,
在菱形ABCD中,∵∠ABC=60°,
∴△ABC、△ACD为正三角形.
∵AC=AD,∠ACE=∠ADF=60°,∠CAE=∠DAF=60°-∠CAF,
∴△AEC≌△AFD(ASA).
∴CE=DF.

(2)结论CE=DF仍然成立,如图④,连接AC,
在菱形ABCD中,∵∠ABC=60°,
∴△ABC、△ACD为正三角形.
∵AC=AD,∠ACB=∠ADC=60°,
∴∠ACE=∠ADF=120°.
∵∠CAE=∠DAF=60°-∠DAE,
∴△ACE≌△ADF(ASA).
∴CE=DF.



科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.

(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则 t的值为 秒(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,试探索:在旋转过程中,∠AOM与∠NOC的差是否发生变化?若不变,请求出这个差值;若变化,请求出差的变化范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)小海喜欢研究数学问题,在计算整式加减(﹣4x2﹣7+5x)+(2x+3x2)的时候,想到了小学的列竖式加减法,令A=﹣4x2﹣7+5x,B=2x+3x2,然后将两个整式关于x进行降幂排列,A=﹣4x2+5x﹣7,B=3x2+2x,最后只要写出其各项系数对齐同类项进行竖式计算如下:
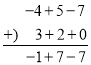
所以,(﹣4x2﹣7+5x)+(2x+3x2)=﹣x2+7x﹣7.
(模仿解题)若A=﹣4x2y2+2x3y﹣5xy3+2x4,B=3x3y+2x2y2﹣y4﹣4xy3,请你按照小海的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数进行竖式计算A﹣B,并写出A﹣B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形中,第(1)个图形由4条线段组成,第(2)个图形由10条线段组成,第(3)个图形由18条线段组成,…………第(6)个图形由( )条线段组成.

A.24B.34C.44D.54
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①![]() .
.
②﹣12020+24÷(﹣2)3﹣32×(![]() )2.
)2.
(2)化简求值:①![]()
②先化简,再求值:2(x3﹣2y2)﹣(x﹣2y)﹣(x﹣3y2+2x3),其中x=﹣3,y=﹣2.
(3)解方程:① 3(x﹣3)+1 = x﹣(2x﹣1)
②![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,AB∥CD∥EF,点G、P、H分别在直线AB、CD、EF上,连结PG、PH,当点P在直线GH的左侧时,试说明∠AGP+∠EHP=∠GPH.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式).

解:如图①,∵AB∥CD( )
∴∠AGP=∠GPD
∵CD∥EF
∴∠DPH=∠EHP( )
∵∠GPD+∠DPH=∠GPH,
∴∠AGP+∠EHP=∠GPH( )
拓展:将图①的点P移动到直线GH的右侧,其他条件不变,如图②.试探究∠AGP、∠EHP、∠GPH之间的关系,并说明理由.
应用:如图③,AB∥CD∥EF,点G、H分别在直线AB、EF上,点Q是直线CD上的一个动点,且不在直线GH上,连结QG、QH.若∠GQH=70°,则∠AGQ+∠EHQ= 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明∠A+∠B=∠C+∠D;
【简单应用】
(2)如图2,AP、CP分别平分∠BAD.∠BCD,若∠ABC=36°,∠ADC=16°,
求∠P的度数;
【问题探究】
(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想∠P的度数,并说明理由.


【拓展延伸】
(4)在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
∠CDB,试问∠P与∠C、∠B之间的数量关系为: ______ (用α、β表示∠P,不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com