
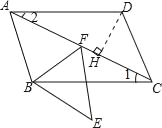
【题目】如图,点F在ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,sin∠CBE=![]() ,求AC的长.
,求AC的长.

【答案】(1)见解析;(2)![]()
【解析】
(1)由外角的性质可得∠AFB=∠FBC+∠FCB,又因为∠ABF=∠FBC+∠FCB,易得AB=AF,由菱形的判定定理可得结论;
(2)作DH⊥AC于点H,由特殊角的三角函数可得∠CBE=30°,由平行线的性质可得∠2=∠CBE=30°,利用锐角三角函数可得AH,DH,由菱形的性质和勾股定理得CH,得AC.
(1)证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形.
∵∠ABF=∠FBC+∠FCB,∠AFB=∠FBC+∠FCB,
∴∠ABF=∠AFB,
∴AB=AF,
∴ABEF是菱形;
(2)作DH⊥AC于点H,
∵![]() ,
,
∴∠CBE=30°,
∵BE∥AC,
∴∠1=∠CBE,
∵AD∥BC,
∴∠2=∠1,
∴∠2=∠CBE=30°,
Rt△ADH中,![]() ,
,
DH=ADsin∠2=4,
∵四边形ABEF是菱形,
∴CD=AB=BE=5,
Rt△CDH中,![]() ,
,
∴![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点为A(-3,-3),此抛物线交x轴于O、 B两点.

(1)求此抛物线的解析式.
(2)求△AOB的面积 .
(3)若抛物线上另有点P满足S△POB=S△AOB,请求出P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+a与x轴交于点A(4,0),与y轴交于点B,抛物线y=
x+a与x轴交于点A(4,0),与y轴交于点B,抛物线y=![]() x2+bx+c经过点A,B.点M(m,0)为x轴上一动点,过点M且垂直于x轴的直线分别交直线AB及抛物线于点P,N.
x2+bx+c经过点A,B.点M(m,0)为x轴上一动点,过点M且垂直于x轴的直线分别交直线AB及抛物线于点P,N.
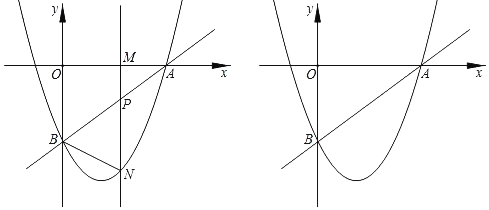
(1)填空:点B的坐标为 ,抛物线的解析式为 ;
(2)当点M在线段OA上运动时(不与点O,A重合),
①当m为何值时,线段PN最大值,并求出PN的最大值;②求出使△BPN为直角三角形时m的值;
(3)若抛物线上有且只有三个点N到直线AB的距离是h,请直接写出此时由点O,B,N,P构成的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
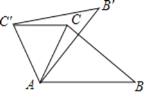
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知![]() ,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.
,对应的坐标如下,请利用学过的变换(平移、旋转、轴对称)知识经过若干次图形变化,使得点A与点E重合、点B与点D重合,写出一种变化的过程_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有不重合的两个点Q(x1,y1)与P(x2,y2).若Q,P为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x轴或y轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“折距”,记做DPQ.特别地,当PQ与某条坐标轴平行(或重合)时,线段PQ的长即点Q与点P之间的“折距”.例如,在图1中,点P(1,-1),点Q(3,-2),此时点Q与点P之间的“折距”DPQ=3.
(1)①已知O为坐标原点,点A(3,-2),B(-1,0),则DAO=______,DBO=______.
②点C在直线y=-x+4上,请你求出DCO的最小值.
(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=3x+6上以动点.请你直接写出点E与点F之间“折距”DEF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣2,3),(3,2),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长为6m的铝合金条制成“日”字形窗框,若窗框的宽为xm,窗户的透光面积为ym2(铝合金条的宽度不计).
(1)求出y与x的函数关系式;
(2)如何安排窗框的长和宽,才能使得窗户的透光面积最大?并求出此时的最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线y=ax2+bx+c的图象经过(﹣1,0),对称轴x=1,则下列三个结论:①abc<0;②10a+3b+c>0;③am2+bm+a≥0.正确的结论为_____(填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com