
 已知△ABC中,AB=1,BC=4$\sqrt{\frac{1}{2}}$,CA=$\frac{1}{5}$$\sqrt{125}$.
已知△ABC中,AB=1,BC=4$\sqrt{\frac{1}{2}}$,CA=$\frac{1}{5}$$\sqrt{125}$.分析 (1)根据二次根式的化简方法进行化简;
(2)根据勾股定理计算边长的方法,在网格中表示AC、BC的长;
(3)由图中可以看出BC边上的高为面积为1的边长为$\sqrt{5}$的边上的高,利用三角形的面积公式可求解.
解答 解:(1)4$\sqrt{\frac{1}{2}}$=2$\sqrt{2}$,$\frac{1}{5}$$\sqrt{125}$=$\sqrt{5}$;
(2)如图所示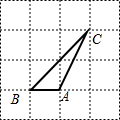
(2)∵△ABD的面积为1,BC=2$\sqrt{2}$,
∴BC边上的高为1×2÷2$\sqrt{2}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了二次根式的化简运算,网格中表示线段长为二次根式的方法,培养学生动手操作能力.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | n≥-$\frac{1}{4}$,且n≠0 | B. | n≥-$\frac{1}{4}$ | C. | n≤-$\frac{1}{4}$ | D. | n≤-$\frac{1}{4}$,且n≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
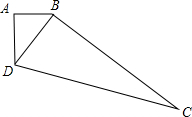 如图是一个四边形的边角料,木工师傅通过测量,获得了如下数据:AB=3cm,BC=12cm,CD=13cm,AD=4cm,BD=5cm木工师傅由此认为这个四边形中∠A恰好是直角,你认为木工师傅的判断正确吗?如果你认为他正确,请说明其中的理由;如果你认为他不正确,那你认为需要什么条件,才可以判断∠A是直角?请求出木料的面积.
如图是一个四边形的边角料,木工师傅通过测量,获得了如下数据:AB=3cm,BC=12cm,CD=13cm,AD=4cm,BD=5cm木工师傅由此认为这个四边形中∠A恰好是直角,你认为木工师傅的判断正确吗?如果你认为他正确,请说明其中的理由;如果你认为他不正确,那你认为需要什么条件,才可以判断∠A是直角?请求出木料的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com