
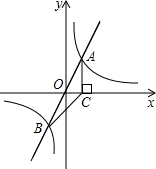
 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=| k |
| x |
| k |
| x |
| k |
| x |
| 8 |
| x |
| 1 |
| 2 |
| 4 |
| 5 |
| 4 |
| 3 |


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为查看答案和解析>>
科目:初中数学 来源: 题型:
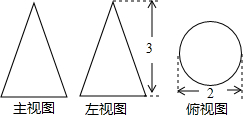 如图是某几何体的三视图,则对该几何体描述正确的是( )
如图是某几何体的三视图,则对该几何体描述正确的是( )| A、它是一个底面直径为2,高为3的圆柱 |
| B、它是一个底面积为π,高为3的圆锥 |
| C、它是一个底面积为4π,高为3的圆锥 |
| D、它是一个底面直径为3,高为2的圆柱 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )
如图,矩形AEHC是由三个全等矩形拼成的,AH与BE、BF、DF、DG、CG分别交于点P、Q、K、M、N.设△BPQ,△DKM,△CNH的面积依次为S1,S2,S3.若S1+S3=20,则S2的值为( )| A、6 | B、8 | C、10 | D、12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
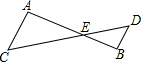 如图,已知△ACE∽△BDE,∠A=117°,∠C=37°,AC=6,BD=3,AB=12,CD=18,(1)求∠B和∠D的度数;
如图,已知△ACE∽△BDE,∠A=117°,∠C=37°,AC=6,BD=3,AB=12,CD=18,(1)求∠B和∠D的度数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com