
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤(a﹣2b+c)<0,其中正确的个数是( )
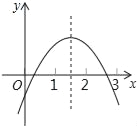
A. 2 B. 3 C. 4 D. 5
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片ABCD对折,使CD与AB重合,得到折痕MN后展开,E为CN上一点,将△CDE沿DE所在的直线折叠,使得点C落在折痕MN上的点F处,连接AF,BF,BD.则下列结论中:①△ADF是等边三角形;②tan∠EBF=2-![]() ;③S△ADF=
;③S△ADF=![]() S正方形ABCD;④BF2=DF·EF.其中正确的是( )
S正方形ABCD;④BF2=DF·EF.其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底点G为BC的中点,则矮建筑物的高CD为( )
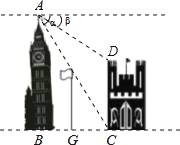
A. 20米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作圆O的切线交边BC于点N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你能发现怎样的结论?
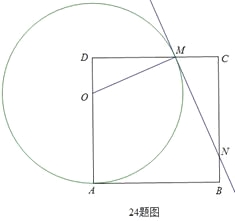
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
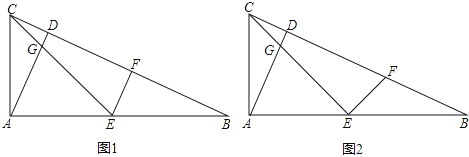
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.
(2)如图2,AC:AB=1:![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与y轴交于点A(0,2),对称轴为直线x=﹣2,平行于x轴的直线与抛物线交于B、C两点,点B在对称轴左侧,BC=6.
(1)求此抛物线的解析式.
(2)点P在x轴上,直线CP将△ABC面积分成2:3两部分,请直接写出P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.
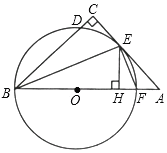
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;
(3)求证:CD=HF.
查看答案和解析>>
科目:初中数学 来源: 题型:
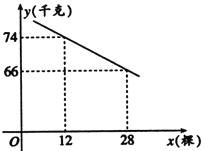
【题目】小丽老师家有一片80棵桃树的桃园,现准备多种一些桃树提高桃园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该桃园每棵桃树产桃![]() (千克)与增种桃树
(千克)与增种桃树![]() (棵)之间的函数关系如图所示.
(棵)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在投入成本最低的情况下,增种桃树多少棵时,桃园的总产量可以达到6750千克?
(3)如果增种的桃树![]() (棵)满足:
(棵)满足: ![]() ,请你帮小丽老师家计算一下,桃园的总产量最少是多少千克,最多又是多少千克?
,请你帮小丽老师家计算一下,桃园的总产量最少是多少千克,最多又是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于点E,垂足为D,连接BE.已知AE=5,tan∠AED=![]() ,求BE+CE的值
,求BE+CE的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com