
【题目】如图,在![]() 中,
中,![]() 是直径,
是直径,![]() 是弦,
是弦,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
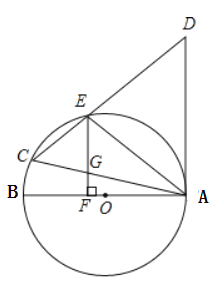
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,已知
,已知![]() ,
,![]() .求
.求![]() 的长;
的长;
(3)在(2)的条件下,求△![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)5;(3)![]() .
.
【解析】
(1)连接BE,由圆周角定理可得∠AEB=90°,∠B+∠EAB=90°,![]() ,从而得到∠DAE+∠EAB=90°,即AD⊥AB,问题得解;
,从而得到∠DAE+∠EAB=90°,即AD⊥AB,问题得解;
(2)延长EF交⊙O于H,证明△EAG∽△CAE,得出![]() ,求出AE长,求出CG=GE=3,则AC=AG+3,可得出
,求出AE长,求出CG=GE=3,则AC=AG+3,可得出![]() ,解出AG=5;
,解出AG=5;
(3)过点G作GM⊥AE,设ME=x,则AM=![]() ,利用勾股定理列方程求ME的长,从而求MG的长,求出△AEG的面积,然后由等高三角形面积比等于底边之比求△ECG得面积,从而使问题得解.
,利用勾股定理列方程求ME的长,从而求MG的长,求出△AEG的面积,然后由等高三角形面积比等于底边之比求△ECG得面积,从而使问题得解.
解:(1)连接BE
在![]() 中,
中,![]() 是直径,
是直径,
∴∠AEB=90°,∠B+∠EAB=90°,![]()
又∵![]()
∴∠DAE+∠EAB=90°,即AD⊥AB
∴![]() 是
是![]() 的切线;
的切线;

(2)延长EF交⊙O于H,
∵EF⊥AB,AB是直径,
∴![]() ,
,
∴∠EBA=∠AEH,
∵∠EAG=∠CAE,
∴△EAG∽△CAE,
∴![]() ,
,
∵AC=AD,
∴∠D=∠C,
∵∠C=∠DAE,
∴∠D=∠DAE,
∴AE=DE=2![]() ,
,
又∠BFE=∠BAD=90°,
∴AD∥EF,
∴∠D=∠CEF,
∴∠C=∠CEF,
∴CG=GE=3,
∴AC=AG+CG=AG+3,
∴![]() ,
,
∴AG=-8(舍)或AG=5,
即AG的长为5.

(3)过点G作GM⊥AE
由(2)可知,AE=![]() ,AG=5,CG=EG=3
,AG=5,CG=EG=3
设ME=x,则AM=![]()
根据勾股定理可得![]() ,解得
,解得![]()
∴MG=![]()
∴![]()
又∵![]()
∴![]()
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量![]() (件),
(件),![]() (件)与加工件的时间
(件)与加工件的时间![]() (天)的函数图象如图所示,
(天)的函数图象如图所示,

(1)乙工厂每天加工零件的数为_____件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量![]() (件)与加工零件的时间
(件)与加工零件的时间![]() (天)的函数关系式,并写出自变量
(天)的函数关系式,并写出自变量![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
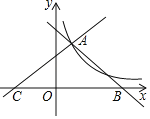
【题目】如图直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,3),这两条直线分别与x轴交于B,C两点.
交于点A(1,3),这两条直线分别与x轴交于B,C两点.
(1)求k的值;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP,且AP把△ABC的面积分成1:2两部分,则此时点P的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
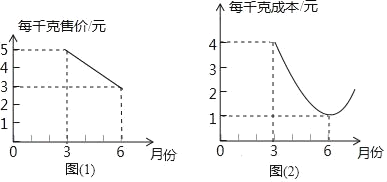
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
(1)求反比例函数的解析式及B点的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.

(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】富贵竹茎叶肥厚,观赏价值高,又有“花开富贵,竹报平安,大吉大利”之意,深受广大花友的喜爱.某花店抓住这个商机,第一次购进![]() 、
、![]() 两种造型的富贵竹共300株.
两种造型的富贵竹共300株.![]() 型富贵竹每盆成本4元,售价8元;
型富贵竹每盆成本4元,售价8元;![]() 型富贵竹每盆成本7元,售价10元.
型富贵竹每盆成本7元,售价10元.
(1)如果第一次购进富贵竹的金额为1500元,那么![]() 型富贵竹购进了多少盆?
型富贵竹购进了多少盆?
(2)富贵竹开始售卖后,十分抢手,花店决定第二次购进这两种造型的富贵竹,它们的进价不变.![]() 型富贵竹的进货量在第一次进货量的基础上增加了
型富贵竹的进货量在第一次进货量的基础上增加了![]() ,售价提高了
,售价提高了![]() ;
;![]() 型富贵竹的售价和进货量不变.结果第二次共获利2100元.求
型富贵竹的售价和进货量不变.结果第二次共获利2100元.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
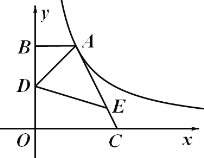
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com