
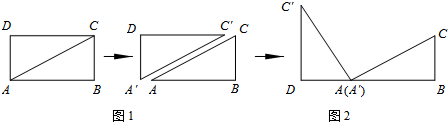
���� ��1��������ת�任�����������BC��ȵ��߶Ρ���CAC��Ķ�����
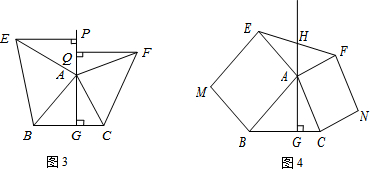
��2������ȫ�������ε��ж����������ʶ���֤����APE�ա�BGA���õ�EP=AG��ͬ��֤��FQ=AG���õ��𰸣�
��3����EP��GA��GA���ӳ�����P����FQ��GA��GA���ӳ�����Q��֤����APE�ס�BGA�͡�AQF�ס�CGA���ɣ�
��� �⣺��1����ͼ2������ת�����ʿ�֪����ABC�ա�A��C��D��
��BC=A��D����ACB=��C��AD���֡�ACB+��CAB=90�㣬
���C��AD+��CAB=90�㣬����CAC��=90�㣬
�ʴ�Ϊ��A��D��=90�㣻
��2��EP=FQ��
֤�����ߡ�ABE�ǵ���ֱ�������Σ�
���EAB=90�㣬����EAP+��BAG=90�㣬�֡�ABG+��BAG=90�㣬
���EAP=��ABG��
�ڡ�APE�͡�BGA�У�
$\left\{\begin{array}{l}{��EAP=��ABG}\\{��APE=��BGA}\\{EA=BA}\end{array}\right.$��
���APE�ա�BGA��
��EP=AG��
ͬ����FQ=AG��
��EP=FQ��
��3��HE=HF��
֤���� ��EP��GA��GA���ӳ�����P����FQ��GA��GA���ӳ�����Q��
��EP��GA��GA���ӳ�����P����FQ��GA��GA���ӳ�����Q��
���ı���ABME�Ǿ��Σ�
���EAB=90�㣬����EAP+��BAG=90�㣬�֡�ABG+��BAG=90�㣬
���EAP=��ABG���֡�APE=��BGA=90�㣬
���APE�ס�BGA��
��$\frac{EP}{AG}=\frac{EA}{AB}$=$\frac{1}{k}$����AG=kEP��
ͬ����AQF�ס�CGA��
��$\frac{AG}{FQ}=\frac{AC}{AF}$=k����AG=kFQ��
��EP=FQ��
��EP��GA��FQ��GA��
��EP��FQ����EP=FQ��
��HE=HF��
���� ���⿼�������ת�����ʣ�ȫ�������ε��ж������ʡ����������ε��ж������ʣ���ȷ���������ߡ����������صĶ����ǽ���Ĺؼ���ע����ת�任�ж�Ӧ�ߡ���Ӧ�ǵ�ȷ����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��2 | B�� | a��-1 | C�� | a��-2 | D�� | a��-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 7 | C�� | 6 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��P�ǵȱ�������ABC��һ�㣬�ҡ�APB����BPC����CPA=3��4��5������PA��PB��PCΪ�ߵ������ε������ڽǵĶ�����
��ͼ��ʾ��P�ǵȱ�������ABC��һ�㣬�ҡ�APB����BPC����CPA=3��4��5������PA��PB��PCΪ�ߵ������ε������ڽǵĶ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com