
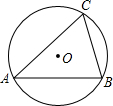
 如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.
如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.  100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
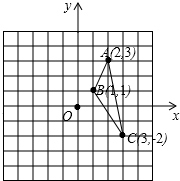 如图,利用关于坐标轴对称的点的坐标特点.
如图,利用关于坐标轴对称的点的坐标特点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
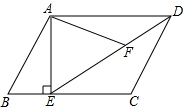 如图,在平行四边形ABCD中,过点F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点F为线段DE上一点,且∠AFE=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
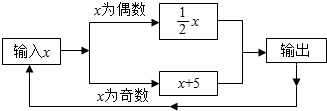 有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2015次输出的结果是4.
有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,依次继续下去…,第2015次输出的结果是4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
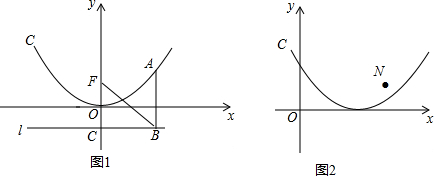
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com