
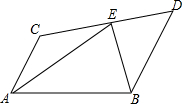
 如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件:
如图,已知梯形ABCD,AC∥BD,点E在CD上,有下列五个条件:分析 在AB上取一点F,使AF=AC,连结EF,就可以得出△ACE≌△AFE,就有∠C=∠AFE.由平行线的性质就有∠C+∠D=180°,由∠AFE+∠EFB=180°得出∠EFB=∠D,再证明△BEF≌△BED,进而就可以得出结论.
解答 组合问题:已知梯形ABCD,AC∥BD,点E在CD上,AE平分∠CAB,BE平分∠DBA;
求证:(1)AB=AC+BD;
(2)AE⊥BE.
证明:在AB上取一点F,使AF=AC,连结EF.
∵EA、EB分别平分∠CAB和∠DBA,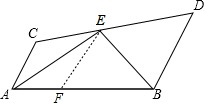
∴∠CAE=∠FAE,∠EBF=∠EBD.
∵AC∥BD,
∴∠C+∠D=180°,
在△ACE和△AFE中,
$\left\{\begin{array}{l}{AC=AF}\\{∠CAE=∠FAE}\\{AE=AE}\end{array}\right.$,
∴△ACE≌△AFE(SAS),
∴∠C=∠AFE,
∵∠AFE+∠EFB=180°,
∴∠EFB=∠D,
在△BEF和△BED中,
$\left\{\begin{array}{l}{∠EFB=∠D}\\{∠EBF=∠EBD}\\{BE=BE}\end{array}\right.$,
∴△BEF≌△BED(AAS),
∴BF=BD,
∵AB=AF+BF,
∴AB=AC+BD;
(2)∵△ACE≌△AFE,
∴∠CEA=∠FEA,
∵△BEF≌△BED,
∴∠FEB=∠DEB,
∴∠AFE+∠FEB=90°,
∴AE⊥BE.
点评 本题考查了平行线的性质的运用,角平分线的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:填空题
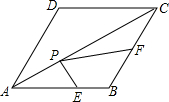 如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.
如图,在菱形ABCD中,AB=10,∠DAB=60°,P是对角线AC上一动点,E、F分别是线段AB和BC上的动点,则PE+PF的最小值是5$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
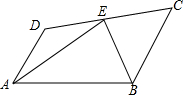 如图,E是线段CD上的一点,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-1|=0.
如图,E是线段CD上的一点,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-1|=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
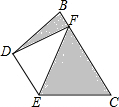 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
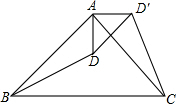 如图,△ABC是等腰直角三角形,BC是斜边,将△ABD绕点A逆时针旋转后,能与△ACD′重合.如果AD=2,那么DD′=2$\sqrt{2}$.
如图,△ABC是等腰直角三角形,BC是斜边,将△ABD绕点A逆时针旋转后,能与△ACD′重合.如果AD=2,那么DD′=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com