
һ�κ�����ͼ��
| һ�κ�����ͼ�� | һ�κ���y=kx+b��ͼ���Ǿ�����(0,�� )��(�� ,0)��һ���� . �ر�أ�����������y=kx��ͼ���Ǿ�����(0���� )��(1���� )��һ���� . |
| ֱ��y=kx+b��y=kx֮��Ĺ�ϵ | ֱ��y=kx+b���Կ�������ֱ��y=kxƽ�Ƶõ���b��0������ ƽ��⑪ ����λ��b��0����⑫ ƽ��⑬ ����λ. |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ƽ��ֱ������ϵ�У���(-3��3)���ڵ�������( )
A.��һ���� B.�ڶ����� C.�������� D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ΰΰ��ѧУ���ٻؼң��յ��ҷ��ֵ���Ҫ��ɵ��Ծ�������ѧУ�����������Ը�����ٶ�ԭ·����ѧУ����һ�龳�У��ٶ�v��ʱ��t�ĺ���ͼ��(������ͼ��˵����)������( )

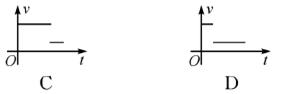
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����ƽ��ֱ������ϵ�У���OΪԲ�ģ��ʵ���Ϊ�뾶��������x���ڵ�M����y���ڵ�N���ٷֱ��Ե�M,NΪԲ�ģ�����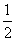 MN�ij�Ϊ�뾶�����������ڵڶ������ڵ�P������P������Ϊ(2a,b+1)����a��b��������ϵΪ( )
MN�ij�Ϊ�뾶�����������ڵڶ������ڵ�P������P������Ϊ(2a,b+1)����a��b��������ϵΪ( )
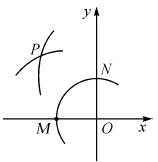
A.a=b B.2a+b=-1 C.2a-b=1 D.2a+b=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����(3��1)��һ�κ���y��kx-2(k��0)��ͼ���ϣ���k��ֵ��( )
A.5 B.4 C.3  D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��������x��y������֮���3���Ӧֵ���±���ʾ��
| x | -1 | 0 | 1 |
| y | -1 | 1 | 3 |
��y��x֮��ĺ�����ϵʽ������( )
A.y=x B.y=2x+1 C.y=x2+x+1 D.y=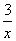
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij�������κϽ��ĵijɱ�y(Ԫ)��������������ȣ���߳�Ϊx���ף���x=3ʱ��y=18����ô���ɱ�Ϊ72Ԫʱ���߳�Ϊ( )
A.6���� B.12���� C.24���� D.36����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com