Question

【题目】如图，在边长为1的小正方形组成的方格纸中，若多边形的每个顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形.记格点多边形内的格点数为，边界上的格点数为，则格点多边形的面积可表示为，其中，为常数.

（1）在下面的两张方格纸中各有一个格点多边形，依次为、正方形.认真数一数：内的格点数是_______，正方形边界上的格点数是_______;

（2）利用（1）中的两个格点多边形确定，的值;

（3）现有一张方格纸共有200个格点，画有一个格点多边形，它的面积，若该格点多边形外的格点数为，求的值.

Answer 1

【答案】(1)3，12；（2）m=1；n=；（3）118.

【解析】

（1）根据题意即可得到结论；

（2）利用已知图形，结合S=ma+nb-1得出关于m，n的关系式，进而求出即可；

（3）首先用a表示出c，然后可求得c-a的值．

（1）△ABC内的格点数是 3，正方形DEFG边界上的格点数是 12；

故答案为：3，12；

（2）∵格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为S=ma+nb-1，其中m，n为常数，

∴三角形：S=3m+8n-1=6，正方形：S=4m+12n-1=9，

则，

解得：；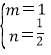

（3）由（2）m=1，n=，

∴S=ma+nb-1=a+b-1

∵格点多边形的面积为40，

∴2a+b-2=80，

∴b=82-2a

∴边界上的格点数与多边形内的格点数的和为b+a=82-2a+a=82-a，

∵总格点数为200，

∴多边形外的格点数c=200-（82-a）=118+a，

∴c-a=118+a-a=118．