
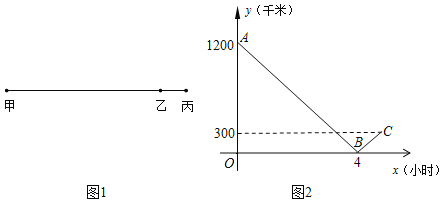
【题目】如图1所示,某乘客乘高速列车从甲地经过乙地到丙地,假设列车匀速行驶.如图2表示列车离乙地路程y(千米)与列车从甲出发后行驶时间x(小时)之间的函数关系图象.
(1)甲、丙两地间的路程为 千米;
(2)求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围;
(3)当行驶时间x为多少时,高速列车离乙地的路程是200千米.
【答案】(1)1500;(2)y=﹣300x+1200(0≤x≤4);y=300x﹣1200(4≤x≤5);(3)x=![]() 或
或![]() .
.
【解析】
(1)由图可知,甲地到乙地距离1200km,乙地与丙地距离300km,进而得到甲、丙间的距离;
(2)先求出列车到达丙地的时间,然后用待定系数法分别求出从甲到乙、从乙到丙时,y与x的函数关系式;
(3)分两种情况,列出方程,即可求解.
解:(1)由函数图象可知,当x=0时y=1200,即刚出发时,甲与乙的距离为1200千米,
当x=4时,y=0,表示,4小时后列车到达乙地,故列车速度为:1200÷4=300千米/小时,
∵300÷300=1小时,∴1小时后列车到达丙地,乙与丙间的距离为300千米,
故甲、丙两地间的距离为:1200+3000=1500千米,
故答案为:1500;
(2)当0≤x≤4时,设函数关系式为:y=k1x+b1,
将(0,1200),(4,0)代入得:
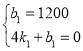 ,
,
解得: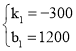 ,
,
∴y=﹣300x+1200;
当4≤x≤5时,设函数关系式为:y=k2x+b2,
将(4,0),(5,300)代入得:
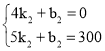 ,
,
解得: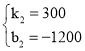 ,
,
∴y=300x﹣1200;
(3)①当0≤x≤4时,200=﹣300x+1200,
∴x=![]()
②当4≤x≤5时,200=300x﹣1200,
解得:x=![]()
综上所述:当x=![]() 或
或![]() 时,高速列车离乙地的路程是200千米.
时,高速列车离乙地的路程是200千米.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有 。
查看答案和解析>>
科目:初中数学 来源: 题型:
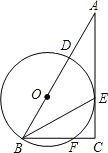
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家出发,外出散步,到一个公共阅报栏前看了一会报后,继续散步了一段时间,然后回家,如图描述了小明在散步过程汇总离家的距离s(米)与散步所用时间t(分)之间的函数关系,根据图象,下列信息错误的是( )

A.小明看报用时8分钟
B.公共阅报栏距小明家200米
C.小明离家最远的距离为400米
D.小明从出发到回家共用时16分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
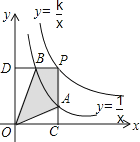
【题目】反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴,交y=
的图象上,PC⊥x轴,交y=![]() 的图象于点A,PD⊥y轴,交y=
的图象于点A,PD⊥y轴,交y=![]() 的图象于点B.当点P在y=
的图象于点B.当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
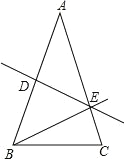
【题目】在△ABC 中,AB>BC,AB=AC,DE 是 AB 的垂直平分线,垂足为 D,交 AC 于 E.
(1)若∠ABE=40°,求∠EBC 的度数;
(2)若△ABC 的周长为 41cm,一边长为 15cm,求△BCE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
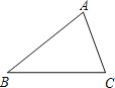
【题目】下面是小芸设计的“作三角形一边上的中线”的尺规作图过程.
已知:△ABC.
求作:BC边上的中线AD.
作法:
(1)分别以点B,C为圆心,AC,AB长为半径画弧,
两弧相交于P点;
(2)作直线AP,AP与BC交于D点.
线段AD就是所求作的BC边上的中线.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接BP,CP,
∵AB=CP,AC=______,
∴四边形ABPC是平行四边形,(______)(填推理的依据)
∴BD=DC,(______)(填推理的依据)
即线段AD是BC边上的中线.
查看答案和解析>>
科目:初中数学 来源: 题型:
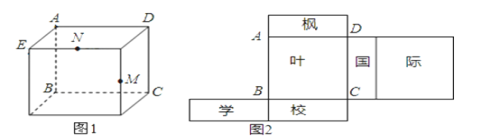
【题目】如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面什么?
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部![]() , 颖颖的头顶
, 颖颖的头顶![]() 及亮亮的眼睛
及亮亮的眼睛![]() 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置![]() ,
, ![]() . 然后测出两人之间的距离
. 然后测出两人之间的距离![]() , 颖颖与楼之间的距离
, 颖颖与楼之间的距离![]() (
(![]() ,
, ![]() ,
, ![]() 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高![]() , 亮亮蹲地观测时眼睛到地面的距离
, 亮亮蹲地观测时眼睛到地面的距离![]() . 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
. 你能根据以上测量数据帮助他们求出住宅楼的高度吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com