
分析 (1)先分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)(3x+1)2-25=0,
(3x+1+5)(3x+1-5)=0
3x+1+5=0,3x+1-5=0,
x1=-2,x2=$\frac{4}{3}$;
(2)2x2-4x=3,
x2-2x=$\frac{3}{2}$,
x2-2x+1=$\frac{3}{2}$+1,
(x-1)2=$\frac{5}{2}$,
x-1=$±\sqrt{\frac{5}{2}}$,
x1=$\frac{2+\sqrt{10}}{2}$,x2=$\frac{2-\sqrt{10}}{2}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 打开电视机,它正在播新闻 | |
| B. | 度量三角形的内角和,结果是180° | |
| C. | 一个袋中装有6个黑球,从中摸出一个白球 | |
| D. | 抛掷5枚硬币,结果是3个正面朝上与3个反面朝上 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
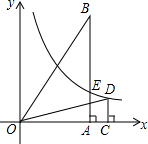 如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,点B的坐标为(5,12),∠BAO=∠OCD=90°,点D在第一象限,OD=6.5,函数y=$\frac{k}{x}$(x>0)的图象经过点D,交AB边于点E.
如图,在平面直角坐标系中,△OBA∽△DOC,边OA、OC都在x轴的正半轴上,点B的坐标为(5,12),∠BAO=∠OCD=90°,点D在第一象限,OD=6.5,函数y=$\frac{k}{x}$(x>0)的图象经过点D,交AB边于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
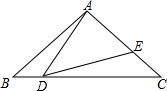 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与B、C两点重合),连接AD,作∠ADE=40°,连接AD,作∠ADE=40°,DE交线段AC于点E.
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与B、C两点重合),连接AD,作∠ADE=40°,连接AD,作∠ADE=40°,DE交线段AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com