
分析 (1)设捐赠物品体育用品x件,则书有(150+x)件,根据等量关系:按书、体育用品进行分类打包,统计得共820件,列出方程求解即可;
(2)设学校安排甲两货车x辆,则乙货车(10-x)辆,根据载重量的不等关系,列出不等式即可求解;
(3)分别求出3种方案的总费用,比较大小即可求解.
解答 解:(1)设捐赠物品体育用品x件,则书有(150+x)件,根据题意,得
x+(150+x)=820,
解得:x=335,
所以书有150+335=485(件)
(2)设学校安排甲两货车x辆,则乙货车(10-x)辆,根据题意,得
$\left\{\begin{array}{l}{100x+30(10-x)≥485}\\{20x+50(10-x)≥335}\end{array}\right.$,
解这个不等式组得$\frac{37}{14}$≤x≤$\frac{11}{2}$,
∵x为整数,
∴①学校安排甲两货车3辆,乙货车7辆;
②学校安排甲两货车4辆,乙货车6辆;
③学校安排甲两货车5辆,乙货车5辆;
(3)①学校安排甲货车3辆,乙货车7辆,
费用800×3+600×7=6600(元);
②学校安排甲货车4辆,乙货车6辆,
费用800×4+600×6=6800(元);
③学校安排甲货车5辆,乙货车5辆,
费用800×5+600×5=7000(元);
∵7000>6800>6600,
∴选择学校安排甲货车3辆,乙货车7辆哪方案可使总费用最少,最少费用是6600元.
点评 本题考查一元一次方程的应用和一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:选择题
| A. | 5.0<m<5.1 | B. | 5.1<m<5.2 | C. | 5.2<m<5.3 | D. | 5.3<m<5.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
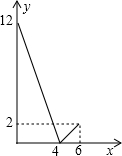 甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.
甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
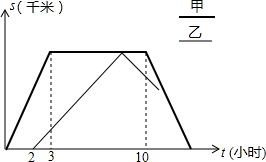 甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:
甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
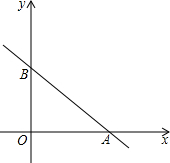 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com