如图，已知在Rt△OAC中，O为坐标原点，直角顶点C在x轴的正半轴上，反比例函数
（k≠0）在第一象限的图象经过OA的中点B，交AC于点D，连接OD．若△OCD∽△ACO，则直线OA的解析式为 ．
黄冈天天练口算题卡系列答案科目：初中数学 来源： 题型：
给出定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．
（1）在你学过的特殊四边形中，写出两个勾股四边形的名称；
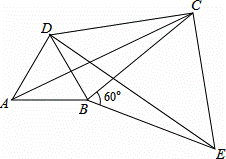
（2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，连接AD、DC、CE，当∠DCB＝30°，求证：四边形ABCD是勾股四边形．
查看答案和解析>>
科目：初中数学 来源： 题型：
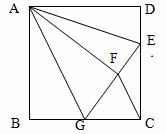
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3D
E．将△ADE沿A
E对折至△AFE，延长EF交边BC于点G，连接AG、CF．则下列结论：①△ABG≌△AFG；②BG=CG；③AG∥CF；④S△EGC=S△AFE；⑤∠AGB+∠AED=145°．其中正确的个数是（ ）
A．2 B．3 C．4 D．5
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系xOy中，已知点M0的坐标为（1，0），将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1；又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2；如此下去，得到线段OM3，OM4，OM5，…
根据以上规律，请直接写出OM2014的长度为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，在平面直角坐标系中，A是抛物线
上的一个动点，且点A在第一象限内．AE⊥y轴于点E，点B坐标为（0，2），直线AB交
轴于点C，点D与点C关于y轴对称，直线DE与AB相交于点F，连结BD．设线段AE的长为m，△BED的面积为S．
（1）当
时，求S的值．
（2）求S关于
的函数解析式．
（3）①若S＝
时，求
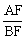的值；
②当m＞2时，设
，猜想k与m的数量关系并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
为创建国家级文明卫生城市，搞好“大美伊春，天然氧吧”的宣传活动，我市园林部门计划用不超过2950盆甲种花卉和2470盆乙种花卉，组建中、小型两类盆景50个．已知组建一个中型盆景需甲种花卉75盆，乙种花卉45盆；组建一个小型盆景需甲种花卉35盆，乙种花卉55盆．
（1）问符合题意的组建方案有几种？请你帮园林部门设计出来；
（2）若组建一个中型盆景的费用是920元，组建一个小型盆景的费用是630元，试说明在（1）中哪种方案费用最低？最低费用是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.∵△OCD∽△ACO，∴
. ∴点A的坐标为（a，
）.∵点B是OA的中点，∴点B的坐标为
.∵点B在反比例函数图象上，∴
，∴a2=2k. ∴点B的坐标为（
，a）.设直线OA的解析式为y=mx，则m·
=a，∴m=2.∴直线OA的解析式为y=2x．
，y2) 在二次函数
的图象上，则 y1 y2(填“>”、“＝”或 “<”)．
的解为