
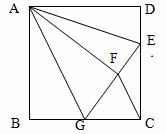
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3D E.将△ADE沿A
E.将△ADE沿A E对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )
E对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤∠AGB+∠AED=145°.其中正确的个数是( )
A.2 B.3 C.4 D.5
C
【解析】① 正确.理由:
正确.理由:
∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴Rt△ABG≌Rt△AFG(HL);
②正确.理由:
EF=DE= CD=
CD= 2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.∴BG=3=6﹣3=GC;
2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.∴BG=3=6﹣3=GC;
③正确.理由:
∵CG=BG,BG=GF,∴CG=GF,∴△FGC是等腰三角形,∠GFC=∠GCF.又∵Rt△ABG≌Rt△AFG;∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°﹣∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;
④正确.理由:
∵S△GCE=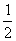 GC•CE=
GC•CE=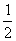 ×3×4=6,∵S△AFE=
×3×4=6,∵S△AFE=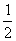 AF•EF=
AF•EF=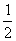 ×6×2=6,∴S△EGC=S△AFE;
×6×2=6,∴S△EGC=S△AFE;
⑤错误.
∵∠BAG=∠FAG,∠DAE=∠FAE,又∵∠BAD=90°,∴∠GAF=45°,∴∠AGB+∠AED=180°﹣∠GAF=135°.
故选C.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
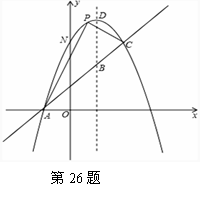
如图,已知抛物线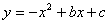 与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)设点M(3,m),求使MN+MD的值最小时m的值;
(3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;
(4)若P是抛物线上位于直线AC上方的一个动点,求△APC的面 积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
A.y=3(x+1)2+2 B.y=3(x+1)2﹣2
C.y=3(x﹣1)2+2 D.y=3(x﹣1)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC比∠BCO的3倍少20°, 则∠D等于( )
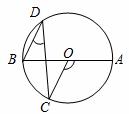
A. 20 B. 25° C. 35° D. 50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com