
【题目】【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF. 
(1).小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF. 小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.
(2).【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;
(3).【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;
(4).【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且ADCE=DEBC,AB=2 ![]() dm,AD=3dm,BD=
dm,AD=3dm,BD= ![]() dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.
dm.M、N分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和. 
【答案】
(1)证明:(小军的方法)连接AP,如图②
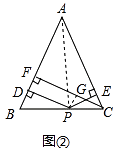
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP+S△ACP,
∴ ![]() ABCF=
ABCF= ![]() ABPD+
ABPD+ ![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD+PE.
(小俊的方法)过点P作PG⊥CF,垂足为G,如图②.
∵PD⊥AB,CF⊥AB,PG⊥FC,
∴∠CFD=∠FDP=∠FGP=90°.
∴四边形PDFG是矩形.
∴DP=FG,∠DPG=90°.
∴∠CGP=90°.
∵PE⊥AC,
∴∠CEP=90°.
∴∠PGC=∠CEP.
∵∠BDP=∠DPG=90°.
∴PG∥AB.
∴∠GPC=∠B.
∵AB=AC,
∴∠B=∠ACB.
∴∠GPC=∠ECP.
在△PGC和△CEP中,
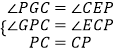
∴△PGC≌△CEP.
∴CG=PE.
∴CF=CG+FG
=PE+PD.
(2)证明:连接AP,如图③.
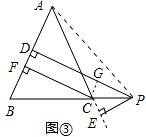
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP﹣S△ACP,
∴ ![]() ABCF=
ABCF= ![]() ABPD﹣
ABPD﹣ ![]() ACPE.
ACPE.
∵AB=AC,
∴CF=PD﹣PE.
(3)过点E作EQ⊥BC,垂足为Q,如图④,
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC﹣CF=AD﹣CF=5.
由折叠可得:DF=BF,∠BEF=∠DEF.
∴DF=5.
∵∠C=90°,
∴DC= ![]()
= ![]()
=4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC.
∴四边形EQCD是矩形.
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB.
∴BE=BF.
由问题情境中的结论可得:PG+PH=EQ.
∴PG+PH=4.
∴PG+PH的值为4.
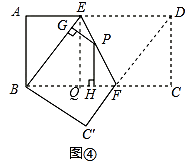
(4)延长AD、BC交于点F,作BH⊥AF,垂足为H,如图⑤.
∵ADCE=DEBC,
∴ ![]() .
.
∵ED⊥AD,EC⊥CB,
∴∠ADE=∠BCE=90°.
∴△ADE∽△BCE.
∴∠A=∠CBE.
∴FA=FB.
由问题情境中的结论可得:ED+EC=BH.
设DH=xdm,
则AH=AD+DH=(3+x)dm.
∵BH⊥AF,
∴∠BHA=90°.
∴BH2=BD2﹣DH2=AB2﹣AH2.
∵AB=2 ![]() ,AD=3,BD=
,AD=3,BD= ![]() ,
,
∴( ![]() )2﹣x2=(2
)2﹣x2=(2 ![]() )2﹣(3+x)2.
)2﹣(3+x)2.
解得:x=1.
∴BH2=BD2﹣DH2
=37﹣1=36.
∴BH=6dm.
∴ED+EC=6.
∵∠ADE=∠BCE=90°,
且M、N分别为AE、BE的中点,
∴DM=M=EM= ![]() AE,CN=BN=EN=
AE,CN=BN=EN= ![]() BE.
BE.
∴△DEM与△CEN的周长之和
=DE+DM+EM+CN+EN+EC
=DE+AE+BE+EC
=DE+AB+EC
=DE+EC+AB
=6+2 ![]() .
.
∴△DEM与△CEN的周长之和为(6+2 ![]() )dm.
)dm.
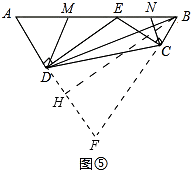
【解析】【问题情境】如下图②,按照小军、小俊的证明思路即可解决问题.【变式探究】如下图③,借鉴小军、小俊的证明思路即可解决问题.【结论运用】易证BE=BF,过点E作EQ⊥BF,垂足为Q,如下图④,利用问题情境中的结论可得PG+PH=EQ,易证EQ=DC,BF=DF,只需求出BF即可.【迁移拓展】由条件ADCE=DEBC联想到三角形相似,从而得到∠A=∠ABC,进而补全等腰三角形,△DEM与△CEN的周长之和就可转化为AB+BH,而BH是△ADB的边AD上的高,只需利用勾股定理建立方程,求出DH,再求出BH,就可解决问题.
【考点精析】解答此题的关键在于理解直角三角形斜边上的中线的相关知识,掌握直角三角形斜边上的中线等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为﹣1. ①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于;
(2)直线y=kx+4(k≠0)与x轴交于点E(x0 , 0),若﹣2<x0<﹣1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连结AP、OP、OA. ①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长;
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2, ![]()
![]()
![]()
![]()
![]()
![]() ,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.
,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度. 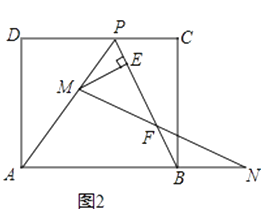
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盐城电视塔是我市标志性建筑之一.如图,在一次数学课外实践活动中,老师要求测电视塔的高度AB.小明在D处用高1.5m的测角仪CD,测得电视塔顶端A的仰角为30°,然后向电视塔前进224m到达E处,又测得电视塔顶端A的仰角为60°.求电视塔的高度AB.( ![]() 取1.73,结果精确到0.1m)
取1.73,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG. 
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中, ①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成). 
选项 | 帮助很大 | 帮助较大 | 帮助不大 | 几乎没有帮助 |
人数 | a | 543 | 269 | b |
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com