Question

在平面直角坐标系xOy中，正方形A₁B₁C₁O、A₂B₂C₂B₁、A₃B₃C₃B₂按图中所示的方式放置，点A₁、A₂、A₃和B₁、B₂、B₃分别在直线y=kx+b和x轴上，若点C₁、C₂的坐标分别是（2，-2）、（7，-3），则点A₃的坐标是

 

．

Answer 1

考点：一次函数图象上点的坐标特征,正方形的性质

专题：规律型

分析：根据正方形的轴对称性，由C₁、C₂的坐标可求A₁、A₂的坐标，将A₁、A₂的坐标代入y=kx+b中，得到关于k与b的方程组，求出方程组的解得到k与b的值，从而求直线解析式，由正方形的性质求出OB₁，OB₂的长，设B₂G=A₃G=t，表示出A₃的坐标，代入直线方程中列出关于b的方程，求出方程的解得到b的值，确定出A₃的坐标．

解答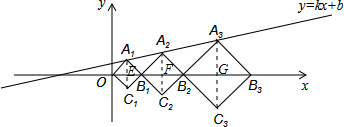：解：连接A₁C₁，A₂C₂，A₃C₃，分别交x轴于点E、F、G，
∵正方形A₁B₁C₁O、A₂B₂C₂B₁、A₃B₃C₃B₂，
∴A₁与C₁关于x轴对称，A₂与C₂关于x轴对称，A₃与C₃关于x轴对称，
∵C₁（2，-2），C₂（7，-3），
∴A₁（2，2），A₂（7，3），
∴OB₁=2OE=4，OB₂=OB₁+2B₁F=4+2×（7-4）=10，
将A₁与A₂的坐标代入y=kx+b中得：

2k+b=2 7k+b=3

，
解得：

k= 1 5 b= 8 5

，
∴直线解析式为y=

1

5

x+

8

5

，
设B₂G=A₃G=t，则有A₃坐标为（10+t，t），
代入直线解析式得：t=

1

5

（10+t）+

8

5

，
解得：t=

9

2

，
∴A₃坐标为（

29

2

，

9

2

）．
故答案是：（

29

2

，

9

2

）．

点评：此题考查了一次函数的性质，正方形的性质，利用待定系数法求一次函数解析式，是一道规律型的试题，锻炼了学生归纳总结的能力，灵活运用正方形的性质是解本题的关键．