
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M,N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,则y关于x的函数图象大致形状是( )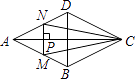
A.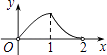
B.
C.
D.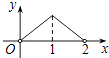
【答案】A
【解析】解:(1)当0<x≤1时,如图1,
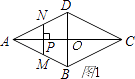
在菱形ABCD中,AC=2,BD=1,AO=1,且AC⊥BD;
∵MN⊥AC,∴MN∥BD;
∴△AMN∽△ABD,
∴ ![]() ,
,
即 ![]() ,
,
∴MN=x,
∴y= ![]() CP×MN=
CP×MN= ![]() (0<x≤1),
(0<x≤1),
∵﹣ ![]() <0,∴函数图象开口向下;(2)当1<x<2,如图2,
<0,∴函数图象开口向下;(2)当1<x<2,如图2,
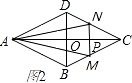
同理证得,△CDB∽△CNM,
![]() ,
,
即 ![]() ,
,
∴MN=2﹣x,
∴y= ![]() CP×MN=
CP×MN= ![]() (2﹣x)×(2﹣x)=
(2﹣x)×(2﹣x)= ![]() ,
,
∵ ![]() >0,
>0,
∴函数图象开口向上;
综上,答案A的图象大致符合;
故答案为:A.
(1)当0<x≤1时,由菱形的性质及平行线分线段成比例得出△AMN∽△ABD,再由相似三角形的性质得出MN=x,再由y= ![]() CP×MN得出解析式,找到图像开口方向;(2)当1<x<2,方法同(1)一样得出MN=2﹣x,再由y=
CP×MN得出解析式,找到图像开口方向;(2)当1<x<2,方法同(1)一样得出MN=2﹣x,再由y= ![]() CP×MN得出解析式,找到图像开口方向;综上所述得出结论。
CP×MN得出解析式,找到图像开口方向;综上所述得出结论。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.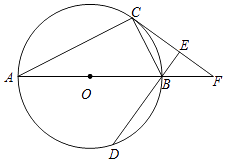
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为时,四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ相交于O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.

(1)如图1,∠BAO=70°,已知AE、BE分别是∠BAO和∠ABO角的平分线,试求出∠AEB的度数.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)在(2)的条件下,在△CDE中,如果有一个角是另一个角的2倍,请直接写出∠DCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠DFB=![]() ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下列空格完成证明:如图, EF∥AD , 1 2 , BAC 70 ,求AGD .
解:∵ EF∥AD ,
∴ 2 .( )
∵ 1 2 ,
∴ 1 3.( )
∴ ∥ .( )
∴ BAC 180 .( )
∵ BAC 70 ,
∴ AGD .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分钟)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?
(4)直角坐标系中的横轴和纵轴上的单位长度取得不一致,这对问题的结论有影响吗?允许这样做吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com