
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
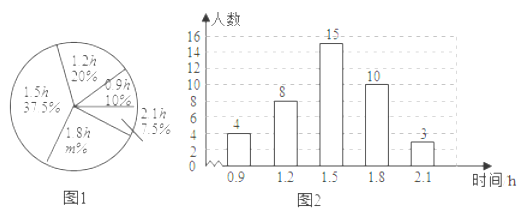
(Ⅰ)本次接受调查的初中学生人数为 ,图1中m的值为 ;
(Ⅱ)求统计的这组每天在校体育活动时间数据的众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有1200名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
【答案】(Ⅰ)40,25;(Ⅱ)众数是1.5,中位数是1.5;(Ⅲ)1080人
【解析】
(Ⅰ)根据统计图中的数据可以求得本次调查的学生人数,进而求得m的值;
(Ⅱ)根据统计图中的数据可以求得这组数据的平均数和众数、中位数;
(Ⅲ)根据统计图中的数据可以求得该校每天在校体育活动时间大于1h的学生人数.
(Ⅰ)本次接受调查的初中学生人数为:4÷10%=40,
m%=![]() =25%,
=25%,
故答案为:40,25.
(Ⅱ)由条形统计图得,4个0.9,8个1.2,15个1.5,10个1.8,3个2.1,
∴1.5出现的次数最多,15次,
∴众数是1.5,
第20个数和第21个数都是1.5,
∴中位数是1.5;
(Ⅲ)1200×![]() =1080(人),
=1080(人),
答:该校每天在校体育活动时间大于1h的学生有1080人.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】某中学举行钢笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图.
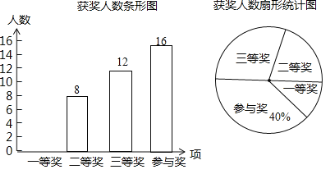
请结合图中相关信息解答下列问题:
(1)扇形统计图中三等奖所在扇形的圆心角的度数是______度;
(2)请将条形统计图补全;
(3)获得一等奖的同学中有![]() 来自七年级,有
来自七年级,有![]() 来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=![]() (x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
(x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
⑴h= ,k= ;
⑵①当点P在顶点时,BC= ;
②BC的值是否随P点横坐标的变化而变化?如果变化,请说明理由,如果不变化,请求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一动点,连接
上一动点,连接![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() 于点
于点 ![]() .
.
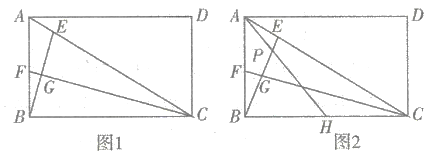
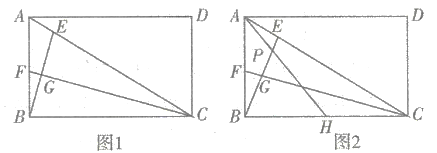
(1)如图1,若![]() 恰好平分
恰好平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于点
于点 ![]() .
.
求证:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一动点,连接
上一动点,连接![]() ,作
,作![]() 分别交
分别交![]() 于点
于点![]() ,
,![]() 于点
于点 ![]() .
.
(1)如图1,若![]() 恰好平分
恰好平分![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 交
交![]() 于点
于点 ![]() .
.
求证:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
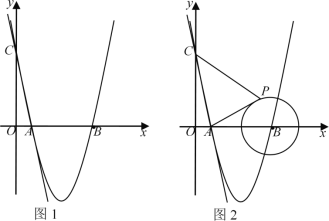
【题目】如图1,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
(1)求抛物线的解析式及![]() 点坐标;
点坐标;
(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC面积最大,求此时点M的坐标及四边形AMBC的面积;
(3)如图2,若![]() 点是半径为2的⊙
点是半径为2的⊙![]() 上一动点,连接
上一动点,连接![]() 、
、![]() ,当点
,当点![]() 运动到某一位置时,
运动到某一位置时,![]() 的值最小为_________.(直接写出结果)
的值最小为_________.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
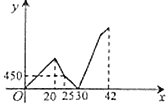
【题目】小杰早上从家匀速步行去学校,走到途中发现英语书忘在家里了,随即打电话给爸爸,爸爸立即送英语书去,小杰掉头以原速往回走,几分钟后,路过一家文具店,此时还未遇到爸爸,小杰便在文具店购买了几个笔记本,刚付完款,爸爸刚好赶到,将英语书交给了小杰(途中小杰打电话、小杰的爸爸找英语书的时间忽略不计):然后,爸爸原速返回,同时小杰把速度提高到原来的![]() 前往学校,爸爸到家后,过一会小杰才到达学校.两人之间的距离
前往学校,爸爸到家后,过一会小杰才到达学校.两人之间的距离![]() (米)与小杰从家出发的时间
(米)与小杰从家出发的时间![]() (分钟)的函数关系如图所示,则家与学校相距______米.
(分钟)的函数关系如图所示,则家与学校相距______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究发现:下面是一道例题及解答过程,请补充完整:
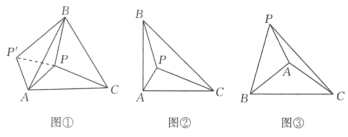
如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形
∴∠APP’=60° ,PA=PP’ ,PC=
∵∠APB=150°,∴∠BPP’=90°
∴P’P2+BP2= ,即PA2+PB2=PC2
(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com