
【题目】为倡导读书风尚,打造书香校园,学校计划购买一批图书。若同时购进![]() 种图书10本和
种图书10本和![]() 种图书7本,共需395元;若同时购进
种图书7本,共需395元;若同时购进![]() 种图书5本和
种图书5本和![]() 种图书3本,共需185元。
种图书3本,共需185元。
(1)求![]() 两种图书的单价各是多少元?
两种图书的单价各是多少元?
(2)若学校计划购买这两种图书共80本,要求每种都要购买,且![]() 种图书的数量少于
种图书的数量少于![]() 种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
种图书的数量,又根据学校预算,购买总金额不能超过1890元,请问学校共有几种购买方案?(请写出具体的购买方案)
【答案】(1)![]() 种图书单价22元,
种图书单价22元,![]() 种图书单价25元;(2)有三种方案
种图书单价25元;(2)有三种方案
【解析】
(1)设购买A种图书每本x元,则购买B种图书每本y元,根据购买A种图书10本、B种图书7本,共用了395元,再根据购买A种图书5本、B种图书3本,共用了185元列出方程组,求解即可;
(2)设购买A种图书m本,根据题意列出不等式解答即可.
(1)设![]() 种图书单价
种图书单价![]() 元,
元,![]() 种图书单价
种图书单价![]() 元,
元,
依题意,得![]() ,解得
,解得![]()
答:![]() 种图书单价22元,
种图书单价22元,![]() 种图书单价25元;
种图书单价25元;
(2)设购买![]() 种图书
种图书![]() 本,则购买
本,则购买![]() 种图书
种图书![]() 本
本
依题意得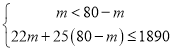
解得![]() ;
;
∵![]() 为正整数,
为正整数,
∴取![]()
∴共有三种方案,方案如下:
购买![]() 种图书37本,则购买
种图书37本,则购买![]() 种图书43本;
种图书43本;
购买![]() 种图书38本,则购买
种图书38本,则购买![]() 种图书42本;
种图书42本;
购买![]() 种图书39本,则购买
种图书39本,则购买![]() 种图书41本.
种图书41本.


科目:初中数学 来源: 题型:
【题目】用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系,寄宿生小红和小敏晚饭后用同一种洗衣粉各自洗一件同样的衣服,漂洗时,小红每次用一盆水(约10升),小敏每次用半盆水(约5升).如果她们都用了5克洗衣粉,第一次漂洗后,小红的衣服中残留的洗衣粉还有1.5克,小敏的衣服中残留的洗衣粉还有2克.
(1)请帮助小红和小敏求出各自衣服中洗衣粉的残留量y与漂洗次数x之间的函数关系式
(2)当洗衣粉的残留量降至0.5克时,便视为衣服漂洗干净,从节约用水的角度来看,你认为谁的漂洗方法值得提倡?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1.
(2)作出△ABC关于原点O成中心对称的△A1B2C2.
(3)请直接写出以A1、B2、C2为顶点的平行四边形的第四个顶点D的坐标________.

查看答案和解析>>
科目:初中数学 来源: 题型:
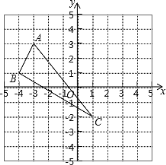
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿![]() 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿![]() 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的![]() (其中
(其中![]() 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);
(2)直接写出![]() 三点的坐标;
三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾不落地,商南更美丽”。某中学为了了解七年级学生对这个一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,将这一情况分为:![]() ——从不随手丢垃圾;
——从不随手丢垃圾;![]() ——偶尔随手丢垃圾;
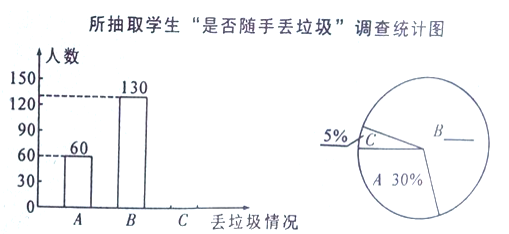
——偶尔随手丢垃圾;![]() ——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题:
(1)补全条形统计图和扇形统计图;
(2)图中“偶尔随手丢垃圾”所在扇形的圆心角为______________;
(3)若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式.
①4×1×2+1=(1+2)2;②4×2×3+1=(2+3)2;③4×3×4+1=(3+4)2…
(1)根据你观察、归纳,发现的规律,写出4×2016×2017+1可以是哪个数的平方?
(2)试猜想第n个等式,并通过计算验证它是否成立.
(3)利用前面的规律,将4(![]() x2+x)(
x2+x)(![]() x2+x+1)+1因式分解.
x2+x+1)+1因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
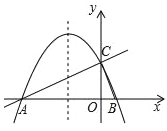
【题目】在如图所示的平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,与x轴的另一交点为点B,其对称轴是
与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,与x轴的另一交点为点B,其对称轴是![]() .
.
(1)求抛物线解析式.
(2)抛物线上是否存在点M(点m不与点C重合),使△MAB与△ABC的面积相等?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
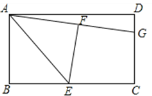
【题目】如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在的直线折叠得到△AFE,延长AF交CD于点G,已知CG=2,DG=1,则BC的长是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.

(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为![]() 秒.
秒.
①若△NPH的面积为1,求![]() 的值;
的值;
②点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com