

分析 (1)根据三角形的面积公式即可求得点C的纵坐标;
(2)根据AE平分∠BAC,可得∠CAE=∠BAE,根据余角的性质即可得出答案;
(3)由于AE平分∠BAC,可得∠CAE=∠BAE,∠ACB=90°,MN⊥AE,从而得出答案.
解答 解:(1)设点C的纵坐标为y,
∵AB=7,S△ABC=14,
∴S△ABC=12×7y=14
∴y=4;
故点C的纵坐标为4;
(2)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠ACB=90°,CF⊥x轴于H,
∴∠CAE+∠CEA=90°,
∴∠EAH+∠AFH=90°,
又∵∠AFH=∠CEF,
∴∠CFE=∠CEF;
(3)证明:∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠ACB=90°,MN⊥AE,
∴∠CAE+∠AEC=90°,
2∠CAE+∠ABC=90°,
∠M+∠AEC=90°,
∴∠ABC=90°-2∠M,
∴∠M、∠ABC之间存在着∠ABC=90°-2∠M这种关系.
点评 本题考查了三角形的面积公式,求点的坐标,角平分线的定义,余角的性质,正确的理解题意,识别图形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
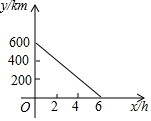 甲、乙两列车分别从A,B两站同时相对开出,甲车每小时行驶60km,如图反映的是从出发到相遇,两车之间的距离y(km)与行驶的时间x(h)之间的函数关系.根据图象回答:
甲、乙两列车分别从A,B两站同时相对开出,甲车每小时行驶60km,如图反映的是从出发到相遇,两车之间的距离y(km)与行驶的时间x(h)之间的函数关系.根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com