
【题目】如图,四边形ABCD是正方形,点A的坐标是(0,1),点B的坐标是(0,﹣2),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过A、C两点,两函数图象的另一个交点E的坐标是(m,3).
的图象经过点C,一次函数y=ax+b的图象经过A、C两点,两函数图象的另一个交点E的坐标是(m,3).
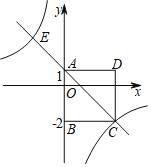
(1)分别求出一次函数与反比例函数的解析式.
(2)求出m的值,并根据图象回答:当x为何值时,一次函数的值大于反比例函数的值.
(3)若点P是反比例函数图象上的一点,△AOP的面积恰好等于正方形ABCD的面积,求点P坐标.
【答案】(1)y=﹣![]() ;y=﹣x+1;(2)x<﹣2或0<x<3;(3)P点坐标为(18,﹣
;y=﹣x+1;(2)x<﹣2或0<x<3;(3)P点坐标为(18,﹣![]() )或(﹣18,
)或(﹣18,![]() )
)
【解析】
(1)先根据A点和B点坐标得到正方形的边长,则BC=3,于是可得到C(3,﹣2),然后利用待定系数法求反比例函数与一次函数的解析式;
(2)将点E的坐标(m,3)代入反比例函数的解析式即可求出m的值,根据图象找出一次函数落在反比例函数图象上方的部分对应的自变量的取值范围即可;
(3)设P(t,﹣![]() ),根据三角形面积公式和正方形面积公式得到
),根据三角形面积公式和正方形面积公式得到![]() ×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
×1×|t|=3×3,然后解绝对值方程求出t即可得到P点坐标.
(1)∵点A的坐标为(0,1),点B的坐标为(0,﹣2),
∴AB=1+2=3,
∵四边形ABCD为正方形,
∴BC=AB=3,
∴C(3,﹣2),
把C(3,﹣2)代入y=![]() ,得k=3×(﹣2)=﹣6,
,得k=3×(﹣2)=﹣6,
∴反比例函数解析式为y=﹣![]() ;
;
把C(3,﹣2),A(0,1)代入y=ax+b,
得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x+1;
(2)∵反比例函数y=﹣![]() 的图象过点E(m,3),
的图象过点E(m,3),
∴m=﹣2,
∴E点的坐标为(﹣2,3);
由图象可知,当x<﹣2或0<x<3时,一次函数落在反比例函数图象上方,
即当x<﹣2或0<x<3时,一次函数的值大于反比例函数的值;
(3)设P(t,﹣![]() ),
),
∵△AOP的面积恰好等于正方形ABCD的面积,
∴![]() ×1×|t|=3×3,解得t=18或t=﹣18,
×1×|t|=3×3,解得t=18或t=﹣18,
∴P点坐标为(18,﹣![]() )或(﹣18,
)或(﹣18,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC⊥AB,连结OC,弦AD∥OC,直线CD交BA的延长线于点E.
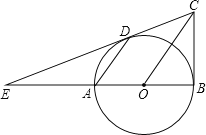
(1)求证:直线CD是⊙O的切线;
(2)若DE=2BC,求AD:OC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注,某校学生会为了解节能减排、垃圾分类知识
的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,
并将检查结果绘制成下面两个统计图.
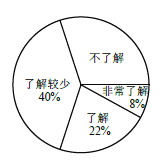

(1)本次调查的学生共有__________人,估计该校1200 名学生中“不了解”的人数是__________人.
(2)“非常了解”的4 人有![]() 两名男生,
两名男生,![]() 两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
两名女生,若从中随机抽取两人向全校做环保交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长是4,点E是AB边上一动点,连接CE,过点B作BG⊥CE于点G,点P是AB边上另一动点,则PD+PG的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.
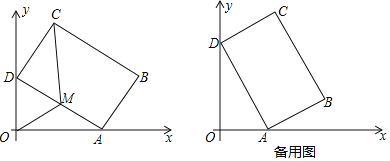
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB//DC,AB=DC,且AB=6cm,BC=8cm,对角线AC =10cm,
(1)求证:四边形ABCD是矩形;
(2)如图(2),若动点Q从点C出发,在CA边上以每秒5cm的速度向点A匀速运动,同时动点P从点B出发,在BC边上以每秒4cm的速度向点C匀速运动,运动时间为t秒(0≤t<2),连接BQ、AP,若AP⊥BQ,求t的值;
(3)如图(3),若点Q在对角线AC上,CQ=4cm,动点P从B点出发,以每秒1cm的速度沿BC运动至点C止.设点P运动了t秒,请你探索:从运动开始,经过多少时间,以点Q、P、C为顶点的三角形是等腰三角形?请求出所有可能的结果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形A1B1C1D1E1F1的边长为1,它的6条对角线围成一个正六边形A2B2C2D2E2F2;正六边形A2B2C2D2E2F2的6条对角线又围成一个正六边形A3B3C3D3E3F3…;如此继续下去,则六边形A4B4C4D4E4F4的面积是_____.
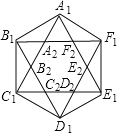
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3![]()
(1)直接写出点B的坐标
(2)已知D.E分别为线段OC.OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式
(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O.D.M.N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com