
【题目】如图1,正方形![]() 中,点
中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 在第一象限.动点
在第一象限.动点![]() 在正方形
在正方形![]() 的边上,从点
的边上,从点![]() 出发沿
出发沿![]() 匀速运动,同时动点
匀速运动,同时动点![]() 以相同速度在
以相同速度在![]() 轴上运动,当点
轴上运动,当点![]() 运动到点
运动到点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() 秒.当点
秒.当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 的横坐标
的横坐标![]() (单位长度)关于运动时间
(单位长度)关于运动时间![]() (秒)的函数图象如图2所示.
(秒)的函数图象如图2所示.
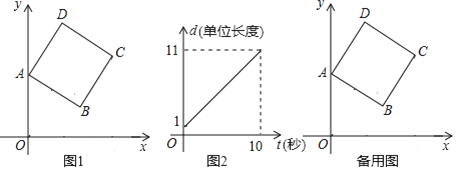
(1)正方形边长![]() _____________,正方形顶点
_____________,正方形顶点![]() 的坐标为__________________;
的坐标为__________________;
(2)点![]() 开始运动时的坐标为__________,点
开始运动时的坐标为__________,点![]() 的运动速度为_________单位长度/秒;
的运动速度为_________单位长度/秒;
(3)当点![]() 运动时,点
运动时,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当点![]() 运动时,过点
运动时,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴,垂足分别为点
轴,垂足分别为点![]() 、
、![]() ,且点
,且点![]() 位于点
位于点![]() 下方,
下方,![]() 与
与![]() 能否相似,若能,请直接写出所有符合条件的
能否相似,若能,请直接写出所有符合条件的![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)10,(14.12);(2)(1,0),1;(3)d=![]() t﹣4;(4)t的值为6s或
t﹣4;(4)t的值为6s或![]() s或
s或![]() s.
s.
【解析】
(1)过点B作BH⊥y轴于点H,CF⊥HB交HB的延长线于点F交x轴于G.利用全等三角形的性质解决问题即可.
(2)根据题意,易得Q(1,0),结合P、Q得运动方向、轨迹,分析可得答案;
(3)分两种情形:①如图3﹣1中,当0<t≤10时,作PN⊥x轴于N,交HF于K.②如图3﹣2中,当10<t≤20时,作PN⊥x轴于N,交HF于K.分别求解即可解决问题.
(4)①如图4﹣1中,当点P在线段AB上时,有两种情形.②如图4﹣2中,当点P在线段BC上时,只有满足![]() 时,△APM∽△PON,利用(3)中结论构建方程即可解决问题.
时,△APM∽△PON,利用(3)中结论构建方程即可解决问题.
解:(1)过点B作BH⊥y轴于点H,CF⊥HB交HB的延长线于点F交x轴于G.
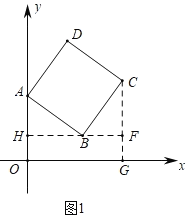
∵∠ABC=90°=∠AHB=∠BFC
∴∠ABH+∠CBF=90°,∠ABH+∠BAH=90°,
∴∠BAH=∠CBF,∵AB=BC,
∴△ABH≌△BCF.
∴BH=CF=8,AH=BF=6.
∴AB=![]() =10,HF=14,
=10,HF=14,
∴OG=FH=14,CG=8+4=12.
∴所求C点的坐标为(14,12).
故答案为10,(14,12)
(2)根据题意,易得Q(1,0),
点P运动速度每秒钟1个单位长度.
故答案为(1,0),1.
(3)①如图3﹣1中,当0<t≤10时,作PN⊥x轴于N,交HF于K.
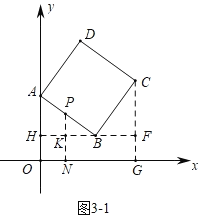
易知四边形OHKN是矩形,可得OH=KN=4,
∵PK∥AH,
∴![]() ,
,
∴![]() ,
,
∴PK=![]() (10﹣t),
(10﹣t),
∴d=PK+KN=﹣![]() t+10.
t+10.
②如图3﹣2中,当10<t≤20时,作PN⊥x轴于N,交HF于K.
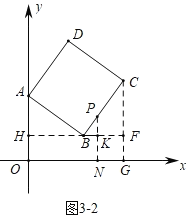
同法可得PK=![]() (t﹣10),
(t﹣10),
∴d=PK+KN=![]() t﹣4.
t﹣4.
(4)①如图4﹣1中,当点P在线段AB上时,有两种情形:
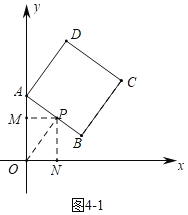
当![]() 时,△APM与△OPN相似,可得
时,△APM与△OPN相似,可得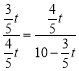 ,
,
解得t=6.
当![]() 时,△APM与△OPN相似,可得
时,△APM与△OPN相似,可得 ,
,
解得t=![]() .
.
②如图4﹣2中,当点P在线段BC上时,只有满足![]() 时,△APM∽△PON,
时,△APM∽△PON,
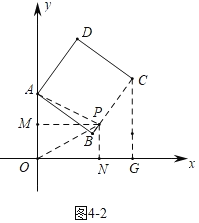
可得:∠OPN=∠PAM=∠AOP,
∵PM⊥OA,
∴AM=OM=PN=5,
由(3)②可知:5=![]() t﹣4,
t﹣4,
解得t=![]() .
.
综上所述,拇指条件的t的值为6s或![]() s或
s或![]() s.
s.


科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)点![]() ,
,![]() 在该函数的图象上,比较
在该函数的图象上,比较![]() 与
与![]() 的大小;
的大小;
(3)将直线![]() 向下平移3个单位,与直线
向下平移3个单位,与直线![]() 交于
交于![]() 点,求点
点,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
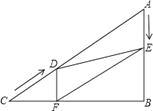
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
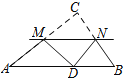
【题目】如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在边AB上的点D处,已知MN∥AB,MC=6,NC=2![]() ,则四边形MABN的面积是___________.
,则四边形MABN的面积是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经营甲、乙两种商品,两种商品的进价和售价情况如下表:
进价(万元/件) | 售价(万元/件) | |
甲 | 12 | 14.5 |
乙 | 8 | 10 |
两种商品的进价和售价始终保持不变.现准备购进甲、乙两种商品共20件.设购进甲种商品![]() 件,两种商品全部售出可获得利润为
件,两种商品全部售出可获得利润为![]() 万元.
万元.
(1)![]() 与
与![]() 的函数关系式为__________________;
的函数关系式为__________________;
(2)若购进两种商品所用的资金不多于200万元,则该公司最多购进多少合甲种商品?
(3)在(2)的条件下,请你帮该公司设计一种进货方案,使得该公司获得最大利润,并求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列格式, ![]() -
- ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)化简以上各式,并计算出结果;
(2)以上格式的结果存在一定的规律,请按规律写出第5个式子及结果.
(3)用含n(n≥1的整数)的式子写出第n个式子及结果,并给出证明的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com