
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.

【答案】![]()
【解析】
】先根据三角形的面积公式求出BM的长,由条件可证得△ABN∽△BNM∽△ABM,且可求得AM=![]() ,利用对应线段的比相等可求得AN和MN,进一步可得到
,利用对应线段的比相等可求得AN和MN,进一步可得到![]() =
=![]() ,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON.
,且∠CAM=∠NAO,可证得△AON∽△AMC,利用相似三角形的性质可求得ON.
∵正方形ABCD的边长为3,S△ABM=![]() ,
,
∴BM=![]() ,
,
∵AB=3,BM=1,
∴AM=![]() ,
,
∵∠ABM=90°,BN⊥AM,
∴△ABN∽△BNM∽△AMB,
∴AB2=AN×AM,BM2=MN×AM,
∴AN=![]() ,MN=
,MN=![]() ,
,
∵AB=3,CD=3,
∴AC=3![]() ,
,
∴AO=![]() ,
,
∵![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,且∠CAM=∠NAO,
,且∠CAM=∠NAO,
∴△AON∽△AMC,
∴![]() =
=![]() =
=![]() ,
,
∴ON=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CFF=45°
(1) 将△ADF绕点A顺时针旋转90 °,得到△ABG(如图1),求证:BE+DF=EF;
(2) 若直线EF与AB、AD的延长线分别交于点M、N(如图2),求证:![]()
(3) 将正方形改为长与宽不相等的矩形,其余条件不变(如图3),直接写出线段EF、BE、DF之间的数量关系.
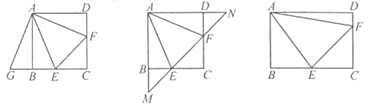
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是平行四边形ABCD对角线BD上的动点,点M为AD的中点,已知AD=8,AB=10,∠ABD=45°,把平行四边形ABCD绕着点A按逆时针方向旋转,点P的对应点是点Q,则线段MQ的长度的最大值与最小值的差为__.
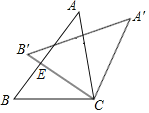
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形![]() 中,点
中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,点
,点![]() 在第一象限.动点
在第一象限.动点![]() 在正方形
在正方形![]() 的边上,从点
的边上,从点![]() 出发沿
出发沿![]() 匀速运动,同时动点
匀速运动,同时动点![]() 以相同速度在
以相同速度在![]() 轴上运动,当点
轴上运动,当点![]() 运动到点
运动到点![]() 时,两点同时停止运动,设运动时间为
时,两点同时停止运动,设运动时间为![]() 秒.当点
秒.当点![]() 在边
在边![]() 上运动时,点
上运动时,点![]() 的横坐标
的横坐标![]() (单位长度)关于运动时间
(单位长度)关于运动时间![]() (秒)的函数图象如图2所示.
(秒)的函数图象如图2所示.
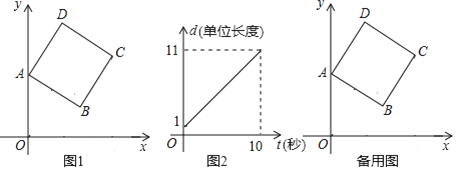
(1)正方形边长![]() _____________,正方形顶点
_____________,正方形顶点![]() 的坐标为__________________;
的坐标为__________________;
(2)点![]() 开始运动时的坐标为__________,点
开始运动时的坐标为__________,点![]() 的运动速度为_________单位长度/秒;
的运动速度为_________单位长度/秒;
(3)当点![]() 运动时,点
运动时,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)当点![]() 运动时,过点
运动时,过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴,垂足分别为点
轴,垂足分别为点![]() 、
、![]() ,且点
,且点![]() 位于点
位于点![]() 下方,
下方,![]() 与
与![]() 能否相似,若能,请直接写出所有符合条件的
能否相似,若能,请直接写出所有符合条件的![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国际上通常用恩格尔系数(记作n)来衡量一个国家和地区人民的生活水平的状况,它的计算公式:n=x/y(x:家庭食品支出总额;y:家庭消费支出总额).各种家庭类型的n如下表:
已知王先生居住地2008年比2003年食品价格上升了25%,该家庭在2008年购买食品和2003年完全相同的情况下多支出2000元,并且y=2x+3600(单位:元),则该家庭2003年属于( )
家庭类型 | 贫困 | 温饱 | 小康 | 富裕 |
n | n>60% | 50%<n≤60% | 40%<n≤50% | 30%<n≤40% |
A. 贫困 B. 温饱 C. 小康 D. 富裕
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AC=BC=2,将一块三角板的直角顶点放在斜边AB的中点P处,将此三角板绕点P旋转,三角板的两直角边分别交射线AC、CB与点D、点E,图①,②,③是旋转得到的三种图形。
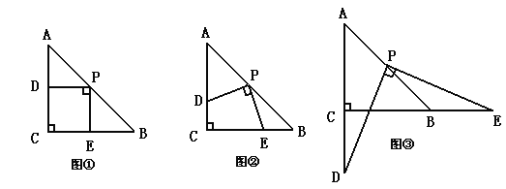
(1)观察线段PD和PE之间的有怎样的大小关系,并以图②为例,加以说明;
(2)△PBE是否构成等腰三角形?若能,指出所有的情况(即求出△PBE为等腰三角形时CE的长,直接写出结果);若不能请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图 1,图 2 都是 8×8 的正方形网格,每个小正方形的边长均为 1,每个小正方形的顶点称为格点.
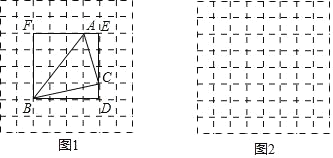
操作发现:小颖在图 1 中画出△ABC,其顶点 A,B,C 都是格点,同时构造正方形 BDEF, 使它的顶点都在格点上,且它的边 DE,EF 分别经过点 C,A,她借助此图求出了△ABC 的面积.
(1)在图 1 中,小颖所画的△ABC 的三边长分别是 AB= ,BC= ,AC
= ;△ABC 的面积为 . 解决问题:
(2)已知△ABC 中,AB=![]() ,BC=2
,BC=2 ![]() ,AC=5
,AC=5 ![]() ,请你根据小颖的思路,在图 2的正方形网格中画出△ABC,并直接写出△ABC 的面积.
,请你根据小颖的思路,在图 2的正方形网格中画出△ABC,并直接写出△ABC 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com