
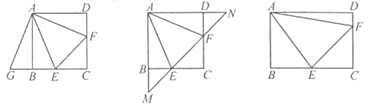
【题目】在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CFF=45°
(1) 将△ADF绕点A顺时针旋转90 °,得到△ABG(如图1),求证:BE+DF=EF;
(2) 若直线EF与AB、AD的延长线分别交于点M、N(如图2),求证:![]()
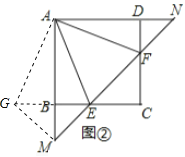
(3) 将正方形改为长与宽不相等的矩形,其余条件不变(如图3),直接写出线段EF、BE、DF之间的数量关系.
【答案】(1)见解析;(2)见解析;(3) ![]() =2
=2![]() .
.
【解析】
(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=![]() DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)延长EF交AB延长线于M点,交AD延长线于N点,将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.由(1)知△AEH≌△AEF,结合勾股定理以及相等线段可得(GH+BE)2+(BE-GH)2=EF2,所以2(DF2+BE2)=EF2.
(1)证明:∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
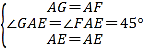 ,
,
∴△AGE≌△AFE(SAS);

(2)证明:设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=![]() DF,
DF,
∴a-BE=a-DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=![]() BM=
BM=![]() DF=NF,
DF=NF,
∴EF2=ME2+NF2;
(3)解:EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM-GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE-GH)2=EF2,
即2(DF2+BE2)=EF2


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】某校组织学生参加“安全知识竞赛”(满分为![]() 分),测试结束后,张老师从七年级
分),测试结束后,张老师从七年级![]() 名学生中随机地抽取部分学生的成绩绘制了条形统计图,如图
名学生中随机地抽取部分学生的成绩绘制了条形统计图,如图![]() 所示.试根据统计图提供的信息,回答下列问题:
所示.试根据统计图提供的信息,回答下列问题:
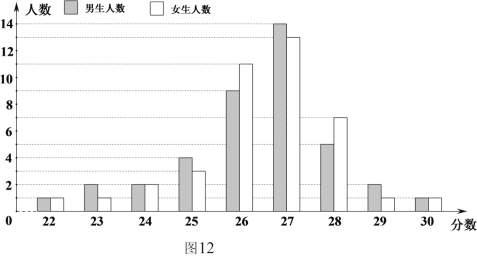
(1)张老师抽取的这部分学生中,共有 名男生, 名女生;
(2)张老师抽取的这部分学生中,女生成绩的众数是 ;
(3)若将不低于![]() 分的成绩定为优秀,请估计七年级
分的成绩定为优秀,请估计七年级![]() 名学生中成绩为优秀的学生人数大约是多少.
名学生中成绩为优秀的学生人数大约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)点![]() ,
,![]() 在该函数的图象上,比较
在该函数的图象上,比较![]() 与
与![]() 的大小;
的大小;
(3)将直线![]() 向下平移3个单位,与直线
向下平移3个单位,与直线![]() 交于
交于![]() 点,求点
点,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第![]() 档次的产品一天的总利润为
档次的产品一天的总利润为![]() 元(其中
元(其中![]() 为正整数,且1≤
为正整数,且1≤![]() ≤10),求出
≤10),求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
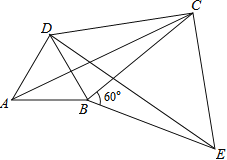
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
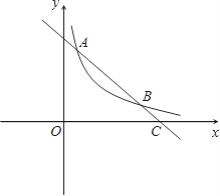
(1)求反比例函数和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
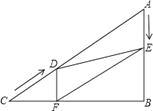
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com