
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图 1,图 2 都是 8×8 的正方形网格,每个小正方形的边长均为 1,每个小正方形的顶点称为格点.
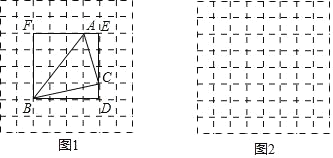
操作发现:小颖在图 1 中画出△ABC,其顶点 A,B,C 都是格点,同时构造正方形 BDEF, 使它的顶点都在格点上,且它的边 DE,EF 分别经过点 C,A,她借助此图求出了△ABC 的面积.
(1)在图 1 中,小颖所画的△ABC 的三边长分别是 AB= ,BC= ,AC
= ;△ABC 的面积为 . 解决问题:
(2)已知△ABC 中,AB=![]() ,BC=2
,BC=2 ![]() ,AC=5
,AC=5 ![]() ,请你根据小颖的思路,在图 2的正方形网格中画出△ABC,并直接写出△ABC 的面积.
,请你根据小颖的思路,在图 2的正方形网格中画出△ABC,并直接写出△ABC 的面积.
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,延长CB至点M,使S△ABM=![]() ,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.
,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形(长方形)ABCD沿EF折叠,使点B与点D重合,点A落在G处,连接BE,DF,则下列结论:①DE=DF,②FB=FE,③BE=DF,④B、E、G三点在同一直线上,其中正确的是( )

A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
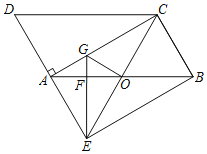
【题目】如图,在平行四边形ABCD中,![]() ,延长DA于点E,使得
,延长DA于点E,使得![]() ,连接BE.
,连接BE.
![]() 求证:四边形AEBC是矩形;
求证:四边形AEBC是矩形;
![]() 过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若
过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,在正方形![]() 中,
中,![]() 是
是![]() 一点,
一点,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,求证:
,求证:![]() ;
;
拓展:在图①中,若![]() 在
在![]() ,且
,且![]() ,则
,则![]() 成立吗?为什么?
成立吗?为什么?
运用:如图②在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
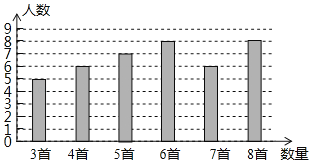
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为_____________,平均数为___________;
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动.
(1)如图1,当点E在边DC上自D向C移动,同时点F在边CB上自C向B移动时,连接AE和DF交于点P,请你写出AE与DF的数量关系和位置关系,并说明理;
(2)如图2,当E,F分别在边CD,BC的延长线上移动时,连接AE,DF,(1)中的结论还成立吗?(请你直接回答“是”或“否”,不需证明);连接AC,求△ACE为等腰三角形时CE:CD的值;
(3)如图3,当E,F分别在直线DC,CB上移动时,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,请你画出点P运动路径的草图.若AD=2,试求出线段CP的最大值.
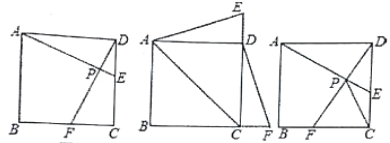
图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com