
【题目】如图所示,一元二次方程x2+2x-3=0的两根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点C,B的横坐标,且此抛物线过点A(3,6)
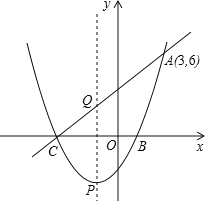
(1)求此抛物线的函数解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC交于点Q,求点P,Q的坐标.
(3)在x轴上是否存在以动点M,使MQ+MA有最小值,若存在求出点M的坐标和最小值,若不存在,请说明理由.
【答案】(1)![]() ;(2)P(﹣1,﹣2),Q(﹣1,2);(3)存在,MQ+MA的最小值为
;(2)P(﹣1,﹣2),Q(﹣1,2);(3)存在,MQ+MA的最小值为![]() .
.
【解析】
(1)先求解方程x2+2x-3=0,得到B,C两点坐标,再设出抛物线的解析式为y=a(x+3)(x﹣1),再将点A(3,6)代入求解即可;
(2)将抛物线解析式化为顶点式得到P点坐标,设直线AC的解析式为y=kx+b,将A,C两点坐标代入得到直线AC的解析式,然后即可求得Q点坐标;
(3)连接AP,与x轴的交点即为所求点M,连接QM,根据点P,Q关于x轴对称,可得此时QM+AM=PM+AM为最小值,设直线AP的解析式为y=ax+c,利用待定系数法求求得直线AP的解析式,得到M点坐标为(0,0),过点A向PQ作垂线,垂足为H,在Rt△AHP中,利用勾股定理即可求得PA的值.
解:(1)解方程x2+2x-3=0,得x1=﹣3,x2=1,
∴交点C(﹣3,0),B(1,0),
设抛物线解析式为y=a(x+3)(x﹣1),
∵点A(3,6)在抛物线上,
∴解得a=![]() ,
,
则抛物线的函数解析式为![]() ;
;
(2)∵![]() ,
,
∴顶点P的坐标为(﹣1,﹣2),对称轴为直线x=﹣1,
设直线AC的解析式为y=kx+b,
∵A(3,6),C(﹣3,0)在直线AC上,
∴![]() ,
,
解得:k=1,b=3,
∴直线AC的解析式为:y=x+3,
当x=﹣1时,y=﹣1+3=2,
∴Q点坐标为(﹣1,2);
(3)存在,理由如下,
∵点P与点Q横坐标相等,纵坐标互为相反数,
∴点P,Q关于x轴对称,
∴连接AP,与x轴的交点即为所求点M,连接QM,
∴QM=PM,
∴QM+AM=PM+AM,
设直线AP的解析式为y=ax+c,
将A(3,6),P(﹣1,﹣2)代入y=ax+c得:
![]() ,
,
解得得a=2,c=0,
∴y=2x,
令y=0,则x=0,
∴点M的坐标为(0,0),
过点A向PQ作垂线,垂足为H,
则AH=4,PH=8,
在Rt△AHP中,![]() ,
,
∴MQ+MA=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,正确的个数为

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+mx的对称轴为直线x=2,若关于x的-元二次方程-x2+mx-t=0 (t为实数)在l<x<3的范围内有解,则t的取值范围是( )
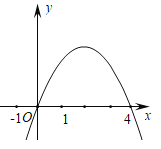
A.-5<t≤4 B.3<t≤4 C.-5<t<3 D.t>-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,两个完全相同的三角形纸片 ABC 和 DEC 重合放置,其中∠C=90°,∠B=∠E=30°.
⑴ 操作发现:如图 2,固定△ABC,使△DEC 绕点 C 旋转,当点 D 恰好落在 AB 边上时, 填空:
①线段 DE 与 AC 的位置关系是 ;
②设△BDC 的面积为 S1,△AEC 的面积为 S2,则 S1 与 S2 的数量关系是 .
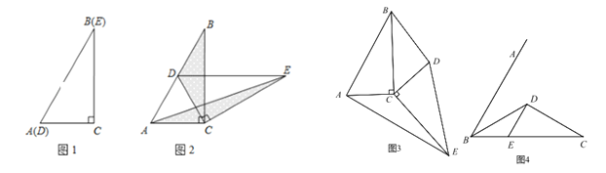
⑵ 猜想论证
当△DEC 绕点 C 旋转到如图 3 所示的位置时,请猜想(1)中 S1 与 S2 的数量关系是否仍 然成立?若成立,请证明;若不成立,请说明理由.
⑶ 拓展探究
已知∠ABC=60°,BD 平分∠ABC,BD=CD,BE=6,DE∥AB 交 BC 于点 E(如图 4).若在射线 BA 上存在点 F,使 S△DCF=S△BDE,请求相应的 BF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
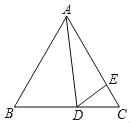
【题目】如图,等边△ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°
(1)求证:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
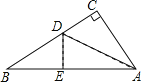
A. 3cmB. 4cmC. 5cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当a>0,b>0时:
∵(![]() )2=a﹣2
)2=a﹣2![]() +b≥0
+b≥0
∴a+b≥2![]() ,当且仅当a=b时取等号.
,当且仅当a=b时取等号.
请利用上述结论解决以下问题:
(1)请直接写出答案:当x>0时,x+![]() 的最小值为 .当x<0时,x+
的最小值为 .当x<0时,x+![]() 的最大值为 ;
的最大值为 ;
(2)若y=![]() ,(x>﹣1),求y的最小值;
,(x>﹣1),求y的最小值;
(3)如图,四边形ABCD的对角线AC、BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.
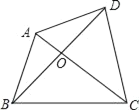
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小华和妈妈到某景区游玩,小明想利用所学的数学知识,估测景区里的观景塔![]() 的高度,他从点
的高度,他从点![]() 处的观景塔出来走到点
处的观景塔出来走到点![]() 处.沿着斜坡
处.沿着斜坡![]() 从
从![]() 点走了
点走了![]() 米到达
米到达![]() 点,此时回望观景塔,更显气势宏伟.在
点,此时回望观景塔,更显气势宏伟.在![]() 点观察到观景塔顶端的仰角为
点观察到观景塔顶端的仰角为![]() 且
且![]() ,再往前走到
,再往前走到![]() 处,观察到观景塔顶端的仰角
处,观察到观景塔顶端的仰角![]() ,测得
,测得![]() 之间的水平距离
之间的水平距离![]() 米,则观景塔的高度
米,则观景塔的高度![]() 约为( ) 米. (
约为( ) 米. (![]() )
)

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com