
【题目】如图,已知一次函数![]() 的图象与x轴、y轴分别交于A、B两点且与反比例函数
的图象与x轴、y轴分别交于A、B两点且与反比例函数![]() 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥![]() 轴于D点,若∠CAD=
轴于D点,若∠CAD=![]() ,AB =
,AB =![]() ,CD =
,CD =![]()
(1)求点A、B、D的坐标;
(2)求一次函数的解析式;
(3)反比例函数的解析式;
(4)求△BCD的面积.

【答案】(1)A(-2,0)B(0,2)C(![]() );(2)y=x+2;(3)
);(2)y=x+2;(3)![]() ;(4)
;(4)![]()
【解析】(1)由题意得到三角形AOB为等腰直角三角形,由斜边求出直角边AO与OB的长,即可确定出A与B的坐标,而三角形ACD为等腰直角三角形,由CD的长求出AD的长,由ADOA求出OD的长,确定出D的坐标;
(2)由C与D的横坐标相同,确定出C的坐标,将A与C的坐标代入一次函数解析式中,求出k与b的值,即可确定出一次函数解析式;
(3)将C的坐标代入反比例解析式中求出m的值,即可确定出反比例解析式;
(4)连接BD,三角形BCD的面积以CD为底,D的横坐标为高,利用三角形的面积公式求出即可.
(1)∵∠CAD=45°,AB=2![]() ,
,
∴AO=BO=2,
∴A(2,0),B(0,2),
∵CD=3.5,
∴AD=3.5,OD=ADOA=3.52=1.5,
∴D(1.5,0),
则C(1.5,3.5);
(2)将A与C坐标代入一次函数解析式得:![]()
解得:![]() ,
,
则一次函数解析式为y=x+2;
(3)将C坐标代入反比例解析式得:1.5=![]() ,即m=
,即m=![]() ,
,
则反比例解析式为y=![]() ;
;
(4)连接BD,

CD=3.5,OD=1.5,
则S△BCD=![]() CD|xD|=
CD|xD|=![]() ×3.5×1.5=
×3.5×1.5=![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】世界上大部分国家都使用摄氏温度(℃),但美国,英国等国家的天气预报都使用华氏温度(℉),两种计量之间有如下对应:
摄氏温度(℃) | … | 0 | 10 | … |
华氏温度(℉) | … | 32 | 50 | … |
已知华氏温度y(℉)是摄氏温度x(℃)的一次函数.
求该一次函数的解析式;
当华氏温度14℉时,求其所对应的摄氏温度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盛盛同学到某高校游玩时,看到运动场的宣传栏中的部分信息(如下表):
院系篮球赛成绩公告 | |||
比赛场次 | 胜场 | 负场 | 积分 |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
盛盛同学结合学习的知识设计了如下问题,请你帮忙完成下列问题:
(1)从表中可以看出,负一场积______分,胜一场积_______分;
(2)某队在比完22场的前提下,胜场总积分能等于其负场总积分的2倍吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6 ![]() ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上. 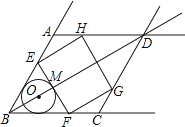
(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24 ![]() 时,求⊙O的半径.
时,求⊙O的半径.
(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个分别含有30°,45°角的一副直角三角板.
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com