
����Ŀ����ͼ��������BA��BC��AD��CDΧ�ɵ�����ABCD�У���ABC=60�㣬AB=6 ![]() ��O������BD��һ�㣬��O��BA��BC�����У���BO���ӳ��߽��ڵ�M����M��EF��BD���߶�BA��������AD���ڵ�E�����߶�BC��������CD���ڵ�F����EFΪ��������EFGH����G��H�ֱ���Χ�����ε��������������ϣ�
��O������BD��һ�㣬��O��BA��BC�����У���BO���ӳ��߽��ڵ�M����M��EF��BD���߶�BA��������AD���ڵ�E�����߶�BC��������CD���ڵ�F����EFΪ��������EFGH����G��H�ֱ���Χ�����ε��������������ϣ� 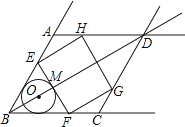
��1����֤��BO=2OM��
��2����EF��HE��������EFGH�����Ϊ24 ![]() ʱ�����O�İ뾶��
ʱ�����O�İ뾶��
��3����HE��HG���O����ʱ�������������������BO�ij���
���𰸡�
��1��
֤������ͼ1��ʾ�����O��AB�ڵ�P������OP�����OPB=90�㣮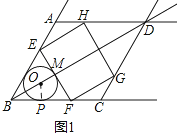
���ı���ABCDΪ���Σ�
���ABD= ![]() ��ABC=30�㣮
��ABC=30�㣮
��OB=2OP��
��OP=OM��
��BO=2OP=2OM��
��2��
�⣺��ͼ2��ʾ����GH��BD�ڵ�N������AC����BD�ڵ�Q��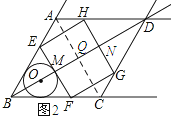
���ı���ABCD�����Σ�
��AC��BD��
��BD=2BQ=2ABcos��ABQ= ![]() AB=18��
AB=18��
���O�İ뾶Ϊr����OB=2r��MB=3r��
��EF��HE��
���E��F��G��H�������εı��ϣ�
����ͼ2��ʾ������E��AB��ʱ��
��Rt��BEM��EM=BMtan��EBM= ![]() r��
r��
�ɶԳ��Եã�EF=2EM=2 ![]() r��ND=BM=3r��
r��ND=BM=3r��
��MN=18��6r��
��S����EFGH=EFMN=2 ![]() r��18��6r��=24
r��18��6r��=24 ![]() ��
��
��ã�r1=1��r2=2��
��r=1ʱ��EF��HE��
��r=1ʱ������������
��r=2ʱ��EF��HE��
���O�İ뾶Ϊ2��
��BM=3r=6��
��ͼ3��ʾ��
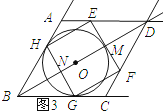
����E��AD����ʱ��BM=3r����MD=18��3r��
�ɶԳ��Կ�֪��NB=MD=6��
��MB=3r=18��6=12��
��ã�r=4��
������������O�İ뾶Ϊ2��4��
��3��
�⣺����GH��BD�ڵ�N����O�İ뾶Ϊr����BO=2r��
����E�ڱ�BA��ʱ����Ȼ������HE��HG���O���У�
����ͼ4��ʾ����E��AD��ʱ��
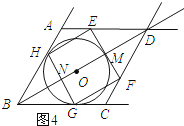
��HE���O����
��ME=r��DM= ![]() r��
r��
��3r+ ![]() r=18��
r=18��
��ã�r=9��3 ![]() ��
��
��OB=18��6 ![]() ��
��
����ͼ5��ʾ��
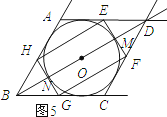
��ͼ�εĶԳ��Եã�ON=OM��BN=DM��
��OB= ![]() BD=9��
BD=9��
����ͼ6��ʾ��
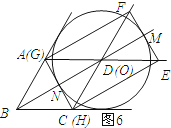
��HG���O����ʱ��MN=2r��
��BN+MN=BM=3r��
��BN=r��
��DM= ![]() FM=
FM= ![]() GN=BN=r��
GN=BN=r��
��D��O�غϣ�
��BO=BD=18��
����ͼ7��ʾ��
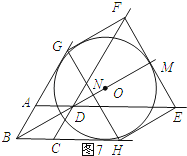
��HE���O����
��EM=r��DM= ![]() r��
r��
��3r�� ![]() r=18��
r=18��
��r=9+3 ![]() ��
��
��OB=2r=18+6 ![]() ��
��
������������HE��GH���O����ʱ��OB�ij�Ϊ18��6 ![]() ��9��18��18+6
��9��18��18+6 ![]() ��
��
����������1�����O��AB�ڵ�P������OP�������ߵ����ʿ�֪��OPB=90�㣮�������ε�������á�OBP�Ķ�����Ȼ�����ݺ�30��ֱ�������ε�����֤�����ɣ�
����������2����GH��BD�ڵ�N������AC����BD�ڵ�Q������������������Ǻ���ֵ���BD�ij������O�İ뾶Ϊr����OB=2r��MB=3r������E��AB��ʱ����Rt��BEM�У���������������Ǻ���ֵ�ɵõ�EM�ij����ú�r��ʽ�ӱ�ʾ������ͼ�εĶԳ��Կɵõ�EF��ND��BM�ij����ú�r��ʽ�ӱ�ʾ���Ӷ��õ�MN=18��6r�����������ݾ��ε�����з�����⼴�ɣ�����E��AD����ʱ��BM=3r����MD=18��3r�������MB=3r=12�з�����⼴�ɣ�
����������3���ȸ������⻭�����������ͼ�Σ�
������������ͼ4��ʾ����E��AD��ʱ�������DM= ![]() r��BM=3r��Ȼ������BM+MD=18���з�����⼴�ɣ�
r��BM=3r��Ȼ������BM+MD=18���з�����⼴�ɣ�
������������ͼ5��ʾ������ͼ�εĶԳ��Կ�֪�õ�OB= ![]() BD��
BD��
������������ͼ6��ʾ����֤��D��O�غϣ��Ӷ������OB�ij���
������������ͼ7��ʾ�������DM= ![]() r��OMB=3r����BM��DM=DB�з�����⼴�ɣ�������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ�������ε����ʡ����ߵ����ʡ�����������Ǻ���ֵ��Ӧ�á����ε������ʽ���������⻭�����������ͼ���ǽ���Ĺؼ���
r��OMB=3r����BM��DM=DB�з�����⼴�ɣ�������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ�������ε����ʡ����ߵ����ʡ�����������Ǻ���ֵ��Ӧ�á����ε������ʽ���������⻭�����������ͼ���ǽ���Ĺؼ���


 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ͨ�˻�������У��������ƽ̨��Ϊ�˽�ҳ�ʹ��ƽ̨�������ѧУ���ҳ���ʹ�������Ϊ������ʹ��������ż��ʹ�á����͡���ʹ�á��������ͣ�������ƽ̨�����ݹ��ܣ����ܳ���У�ˣ�1����Ͱˣ�2����ȫ��ҳ���ʹ������������Ƴ���ͼ��ʾ��������������ͳ��ͼ��

�����ͼ����Ϣ�����������
��1���˴ε���ļҳ�������Ϊ�� ����
��2������ͳ��ͼ�д�������ʹ�á����͵�����Բ�ĽǵĶ������� ���㣬����ȫ����ͳ��ͼ��
��3������У���꼶ѧ���ҳ�����1200�ˣ����ݴ˴ε��������Ƹ�У���꼶�С�����ʹ�á����͵ļҳ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��![]() +����3��2����
+����3��2���� ![]() ��1��0
��1��0![]()
��2������2+m����2��m��+m��m��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪һ�κ���![]() ��ͼ����x�ᡢy��ֱ���A��B�������뷴��������
��ͼ����x�ᡢy��ֱ���A��B�������뷴��������![]() ��ͼ���ڵ�һ������C�㣬CD��
��ͼ���ڵ�һ������C�㣬CD��![]() ����D�㣬����CAD=
����D�㣬����CAD=![]() ��AB =
��AB =![]() ��CD =
��CD =![]()
��1�����A��B��D�����ꣻ
��2����һ�κ����Ľ���ʽ��
��3�������������Ľ���ʽ��
��4������BCD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������ͼ�У�������и��⣨��ֱ��ͼ�������֣�
��1�����������ABC����ֱ��DE�ĶԳƵ���A1B1C1��
��2����DE�ϻ�����P��ʹPA+PC��С��
��3����DE�ϻ�����Q��ʹQA��QB���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ĵ�A��B��C��D����Բ����̶ȵ�ֱ�߰�����Ҫ���벽�軭��ͼ�β����㣺

��1����ֱ��AB��
��2��������DC��
��3���ӳ��߶�DA����E��ʹAE=AB����������ͼ�ۼ���
��4����һ��P��ʹ��P����ֱ��AB�ϣ������߶�CE�ϣ�
��5����AB=2cm��AD=1cm�����߶�DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�����������������Σ�ͼ�Т٢ڢۣ�ƴ����һ��ƽ���ı���ABCD����![]() ����
����![]() =_____ �ȣ�
=_____ �ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�ۿ�Pλ�ڶ�������ĺ������ϣ�A��B�����ִ�ͬʱ�Ӹۿ�P������������һ�̶������У�A�ִ�ÿСʱ����12���B�ִ�ÿСʱ����16��������뿪�ۿ�һ����Сʱ��ֱ�λ�ڵ�R��Q���������30�����֪B�ִ��ر�ƫ��60�㷽���У�
��1��A�ִ����ĸ������У���˵�����ɣ�
��2���������ʱA�ִ��������ߵľ��룮
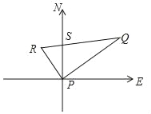
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ĸm��n�Ĵ���ʽ�ǣ�![]() .
.
��1�������������ʽ��
��2��С��ȡm��n��Ϊ������һ����ֵ���뻯��Ĵ���ʽ�У�ǡ�ü���ô���ʽ��ֵ����0.��ôС����ȡ����ĸn��ֵ���ڶ��٣�
��3��������С�Ǵӻ���Ĵ���ʽ�з��֣�ֻҪ��ĸnȡһ���̶�������������ĸmȡ����������ʽ��ֵ��Ϊһ�������������ôС����ȡ����ĸn��ֵ�Ƕ����أ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com