Question

如图，在△ABC中，AB=AC=

3

，D是BC上一点，且AD=1，则BD•DC=

 

．

Answer 1

考点：勾股定理,等腰三角形的性质

专题：

分析：过A点作AE⊥BC于E，根据勾股定理和线段相互间的关系可得AB²=AD²+BD•CD，再把数据代入计算即可求解．

解答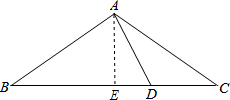：解：过A点作AE⊥BC于E，则
∵AB²=AE²+BE²
=AD²-DE²+BE×CE
=AD²-DE²+（BD-DE）（CD+DE）
=AD²-DE²+BD•CD+BD•DE-CD•DE-DE²
=AD²+BD•CD-DE²×2-CD•DE++（CD+2DE）*DE
=AD²+BD•CD，
∴BD•CD=AB²-AD²=3-1=2．
故答案为：2．

点评：考查了勾股定理和等腰三角形的性质，勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．