
分析 根据分式的性质,可得同分母分式,根据分式的加减,可得答案.
解答 解:当a>b时,$\frac{a}{b}$-$\frac{a+m}{b+m}$=$\frac{ab+am-ab-bm}{b(b+m)}$=$\frac{m(a-b)}{b(b-m)}$>0,
∴$\frac{a}{b}$>$\frac{a+m}{b+m}$;
当a<b时,$\frac{a}{b}$-$\frac{a+m}{b+m}$=$\frac{ab+am-ab-bm}{b(b+m)}$=$\frac{m(a-b)}{b(b-m)}$<0,
∴$\frac{a}{b}$<$\frac{a+m}{b+m}$.
点评 本题考查了分式的加减法,利用作差法是比较分式大小的常用方法,分类讨论是解题关键,以防遗漏.


科目:初中数学 来源: 题型:选择题
| A. | cosA=sinB | B. | sinA=cosB | C. | sin(A+B)=sinC | D. | sinA=sinB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
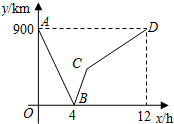 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象解决以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
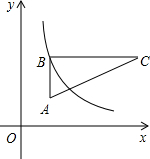 如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC,BA分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,BC=4.
如图,在直角坐标系中,Rt△ABC位于第一象限,两条直角边BC,BA分别平行于x轴、y轴,点A的坐标为(1,1),AB=2,BC=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com