
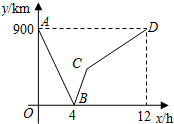
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象解决以下问题:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象解决以下问题:分析 (1)由图象看出两地距离,两车相遇的时间,两车相遇y=0,由图象看出时间t.由v=$\frac{s}{t}$可以求速度.
(2)由函数图象的数据,根据速度=路程÷时间就可以得出慢车的速度,由相遇问题求出速度和就可以求出快车的速度,由快车的速度求出快车走完全程的时间就可以求出点C的横坐标,由两车的距离=速度和×时间就可以求出C点的纵坐标,由待定系数法就可以求出结论.
解答 解:(1)由图形可以看出甲乙两地距离为900km.
当两车相遇y=0,可以由图象知道t=4,
故快车和慢车行驶4h时相遇.
慢车到达甲地需要12小时,由v=$\frac{s}{t}$知,
v=$\frac{900}{12}$=75km/h,故慢车的速度为75km/h.
故答案为12h,75km/h,4h;
(2)线段BC的实际意义是从两车相遇至快车到达乙地的这一时间段里,两车之间的距离.
由题意,得快车与慢车的速度和为:900÷4=225km/h,
慢车的速度为75km/h,
快车的速度为:225-75=150 km/h.
又由于快车行驶900km到达乙地,所以快车行驶$\frac{900}{150}=6(h)$到达乙地.
当x=6时,此时两车之间的距离为6×75=450(km),所以点C的坐标为(6,450).
因为B(4,0),
设线段BC所表示的函数关系式为y=kx+b,把(4,0),(6,450)代入得$\left\{\begin{array}{l}0=4k+b\\ 450=6k+b.\end{array}\right.$解得 $\left\{\begin{array}{l}k=225\\ b=-900.\end{array}\right.$
所以,线段BC所对应的函数关系式为y=225x-900(4≤x≤6).
点评 本题考查了一次函数的应用,行程问题的数量关系路程÷时间=速度的运用,待定系数法求一次函数的解析式的运用,相遇问题的数量关系的运用,解答时求出一次函数的解析式是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 工人师傅要把一根质地均匀的圆柱形木料锯成若干段,按如图的方式锯开,每锯断一次所用的时间相同.若锯成6段需要时间10分钟,则锯成n(n≥2,且n为整数)段所需的时间为( )
工人师傅要把一根质地均匀的圆柱形木料锯成若干段,按如图的方式锯开,每锯断一次所用的时间相同.若锯成6段需要时间10分钟,则锯成n(n≥2,且n为整数)段所需的时间为( )| A. | $\frac{5}{3}$n分钟 | B. | 2n分钟 | C. | (2n+2)分钟 | D. | (2n-2)分钟 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x$≠\frac{3}{2}$ | B. | x≠-1 | C. | x$≠\frac{3}{2}$且x≠-1 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com