
【题目】如图,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() .
.
![]() 尺规作图:作
尺规作图:作![]() 的角平分线BD,交AC于点
的角平分线BD,交AC于点![]() 保留作图痕迹,不写作法
保留作图痕迹,不写作法![]() ;
;
![]() 判断
判断![]() 是否为等腰三角形,并说明理由.
是否为等腰三角形,并说明理由.

【答案】(1)见解析;(2)△BCD是等腰三角形.理由见解析
【解析】
(1)以B为圆心,以任意长为半径画弧交AB、AC于两点,再以这两点为圆心,以大于这两点的距离的一半为半径画弧,交于一点,过这点和B作直线即可;
(2)由∠A=36°,求出∠C、∠ABC的度数,能求出∠ABD和∠CBD的度数,即可求出∠BDC,根据等角对等边即可推出答案.
(1)如图所示:

BD即为所求;
(2)∵AB=AC,
∴∠ABC=∠C,
∵∠A=36°,
∴∠ABC=∠ACB=(180°-36°)÷2=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,
∴∠BDC=36°+36°=72°,
∴BD=BC,
∴△DBC是等腰三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).

(1)求这两个函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角.
(1)如果上述仰角与俯角分别为30。与60。 , 且该楼的高度为30米,求该时刻无人机的竖直高度CD.
(2)如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
(1)求证:△APD≌△CPD.
(2)当菱形ABCD变为正方形,且PC=2,tan∠PFA= ![]() 时,求正方形ABCD的边长.
时,求正方形ABCD的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点,求BC边上的中线AD的取值范围.
,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使![]() ,请补充完整证明“
,请补充完整证明“![]() ≌
≌![]() ”的推理过程.
”的推理过程.
![]() 求证:
求证:![]() ≌
≌![]()
证明:![]() 延长AD到点E,使
延长AD到点E,使![]()
在![]() 和
和![]() 中
中![]() 已作
已作![]() ,
,
![]() ______
______![]() ,
,
![]() 中点定义
中点定义![]() ,
,
![]() ≌
≌![]() ______
______![]() ,
,
![]() 探究得出AD的取值范围是______;
探究得出AD的取值范围是______;
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
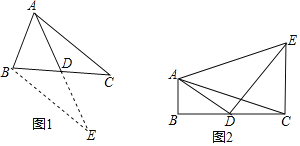
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,AD是
,AD是![]() 的中线,
的中线,![]() ,
,![]() ,且
,且![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:

现有条件下,这15位村民应承包多少公顷土地,怎样安排能使得每人都有事可做,并且资金正好够用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com