
【题目】![]() 如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上的一动点,连接CP并延长交AD于E,交BA的延长线于点F.
(1)求证:△APD≌△CPD.
(2)当菱形ABCD变为正方形,且PC=2,tan∠PFA= ![]() 时,求正方形ABCD的边长.
时,求正方形ABCD的边长.
【答案】
(1)解 :∵四边形ABCD是菱形 ,
∴DC=DA ,∠CDB=∠ADB
,又DP=DP ,
∴△APD≌△CPD.
(2)解 :∵△APD≌△CPD.
∴∠DAP=∠DCP,
∵CD∥BF,
∴∠DCP=∠F,
∴∠DAP=∠F,
又∵∠APE=∠FPA,
∴△APE∽△FPA,
∴AP∶FP=PE∶PA,
∴PA2=PEPF,
∵△APD≌△CPD,
∴PA=PC,
∴PC2=PEPF;
∵tan∠PFA= ![]() ,∠DCP=∠F,
,∠DCP=∠F,
∴tan∠DCP=![]() =
=![]() ,
,
∴DC=2DE ,
∵四边形ABCD是正方形 ,
∴DC=DA ,
∴DA=2DE ,
即点E是DA的中点 ,
∴DE=EA
在DCE与AFE中,
∵∠DCP=∠F
∠DEC=∠AEF
DE=AE
∴DCE≌AFE
∴EC=EF ,设PE=x ,则EC=EF=x+2 ,PF=2X+2
22=X·(2x+2)
解得 x1=-2 (舍去) ,x2=1 ,
∴CE=3 ,
再RtDEC中,设DE=y ,则DC=2y ,根据勾股定理得y2+(2y)2=32
解得 y±=![]() ,∴DE=
,∴DE=![]()
∴DC=![]() ,
,
即正方形的边长为![]()
【解析】(1)根据菱形的性质得出DC=DA ,∠CDB=∠ADB,又DP=DP ,从而利用AAS判断出△APD≌△CPD;
(2)首先由全等三角形的性质得出∠DAP=∠DCP,根据平行线的性质得出∠DCP=∠F,,从而得出∠DAP=∠F,又∠APE=∠FPA,故△APE∽△FPA ,根据相似三角行的性质得出AP∶FP=PE∶PA,即PA2=PEPF,又由全等三角形的性质得出PA=PC,从而得出PC2=PEPF;根据锐角三角函数的定义及等角的同名三角函数值相等得出DC=2DE ,根据正方形的性质得出DE=EA ,然后利用AAS判断出DCE≌AFE ,得出EC=EF ,设PE=x ,则EC=EF=x+2 ,PF=2X+2 ,从而得出关于x的方程求解得出x的值,从而得出CE的长,再RtDEC中,设DE=y ,则DC=2y ,根据勾股定理得出关于y的方程,求解得出y的值,进而得出正方形的边长。
【考点精析】掌握菱形的性质和正方形的性质是解答本题的根本,需要知道菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
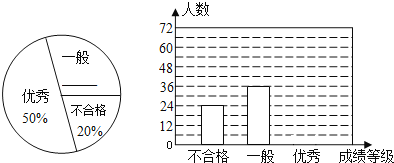
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有学生 2000人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠![]() 是锐角,∠
是锐角,∠![]() 是钝角,且∠
是钝角,且∠![]() +∠
+∠![]() =180°,那么下列结论正确的是( )
=180°,那么下列结论正确的是( )
A. ∠![]() 的补角和∠
的补角和∠![]() 的补角相等 B. ∠
的补角相等 B. ∠![]() 的余角和∠
的余角和∠![]() 的补角相等
的补角相等
C. ∠![]() 的余角和∠
的余角和∠![]() 的补角互余 D. ∠
的补角互余 D. ∠![]() 的余角和∠
的余角和∠![]() 的补角互补
的补角互补
查看答案和解析>>
科目:初中数学 来源: 题型:
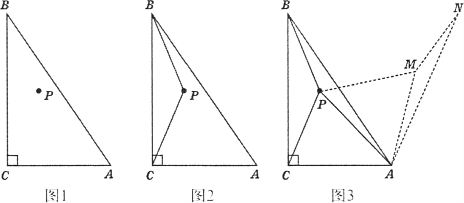
【题目】如图1,在△ABC中,∠ACB=90°,点P为ΔABC内一点.
(1)连接PB,PC,将ABCP沿射线CA方向平移,得到ΔDAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将ΔABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=60°,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于△ABC内一点P,连接PC.
(1)若∠ACP=24°,求∠ABP的度数;
(2)若∠ACP=m°,∠ABP=n°,请直接写出m,n满足的关系式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
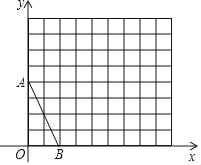
【题目】在平面直角坐标系中,A、B均在边长为1的正方形网格格点上.
(1)求线段AB所在直线的函数解析式,并写出当0≤y≤2时,自变量x的取值范围
(2)将线段AB绕点A逆时针旋转90°,得到线段AC,请在网格中画出线段AC.
(3)若直线AC的函数解析式为y=kx+b,则y随x的增大而 (填“增大”或“减小”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com