
分析 (1)根据题意计算行车情况的和进行判断即可;
(2)根据题意求出每一乘客所付费用求和即可;
(3)算出总里程求出所耗油的费用与收入进行比较即可.
解答 解:(1)-2+5-1+10-3-2-4+6=9(千米).
所以小王在下午出车的出发地的正南方向,距下午出车的出发地9千米;
(2)10+10+2(5-3)+10+10+2(10-3)+10+10+10+2(4-3)+10+2(6-3)=106(元).
所以小王这天下午收到乘客所给车费共106元;
(3)(2+5+1+10+3+2+4+6)×0.3×6
=33×0.3×6
=59.4(元),
106-59.4=46.6(元).
所以小王这天下午盈利,盈利46.6元.
点评 此题主要考查正负数的运用,理解正负数的意义,认真审题明确何时与符号有关系,何时与绝对值有关系是解题的关键.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:填空题
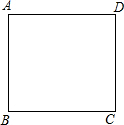 如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2.
如图是一张边长为3cm的正方形纸片ABCD.现要利用这张正方形纸片剪出一个腰长为2cm的等腰三角形,要求等腰三角形的一个顶点与正方形的一个顶点重合,另外两个顶点都在正方形的边上,则剪下的等腰三角形的面积为2或$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
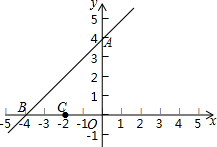 如图,已知直线l的解析式为y=x+4与y轴交于A点,与x轴交于B点.
如图,已知直线l的解析式为y=x+4与y轴交于A点,与x轴交于B点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com